A Constant Proportion Portfolio Insurance Style Trading Strategy
A Pythonic Implementation of Constant Proportion Portfolio Insurance into a Trading Strategy using the Alpaca API


Please note that this article is for educational purposes only. Alpaca does not recommend any specific securities or investment strategies.
A way to protect your investments from systemic risks.
Let’s start by asking you (the reader) a simple question. What are the risks involved with your current investment portfolio? Well, two important risks that investors must be concerned about within their investment portfolio are - Idiosyncratic (or specific) and Systematic (or market) risk.
Idiosyncratic risk: This risk is associated with holding a particular asset like a single company stock, which is also known as company-specific risk or a group of an asset belonging to a similar category like stocks from the same sector, which is also known as sector-specific risk. It can be mitigated with diversification i.e. by reducing exposures to a particular asset or sector and transferring that to some uncorrelated assets or sectors.
Systematic risk: This is a risk associated with the market itself and it cannot be mitigated with diversification. The most popular solution is to hedge against such situations using derivatives like options. Though hedging provides good downside protection, at the same time it also limits the overall portfolio’s upsides, because it's complex and expensive to implement.
By now if you are thinking, is there any other solution that offers good downside protection similar to hedging and also doesn’t limit the upside and is simple to implement? It is too good to be true that in fact there is a very elegant solution and it doesn’t involve derivatives. This opens us to the world of Portfolio Insurance Strategies. In this article, I will discuss portfolio insurance strategies and implement them in Python with Alpaca trade API, along with a live trading algorithm.
CPPI
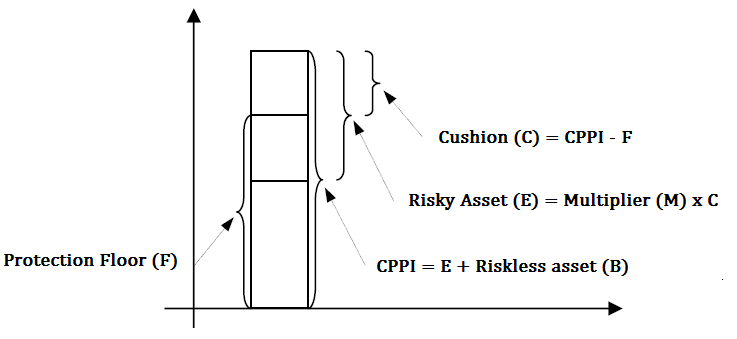
Constant Proportion Portfolio Insurance or CPPI is a portfolio insurance strategy introduced by Black and Jones in 1987. It allows an investor to dynamically allocate assets to get performance by exposing them to the upside while protecting against the downside. The investor sets a floor value on their portfolio, the aim is not to breach that floor value at any time, then he decides how much budget is to be allocated between the two assets. The two asset classes used in CPPI are a risky asset (usually equities or mutual funds) and a conservative asset of either cash, high yield savings account or treasury bonds. The percentage allocated to each depends on the "cushion" value, defined as current portfolio value minus floor value, and a multiplier coefficient, where a higher number denotes a more aggressive strategy.
Algorithm
The CPPI algorithm can be implemented with these simple steps:
- Calculate the cushion \(C = CPPI - F \). Here \(F\) is the pre-defined floor for CPPI.
- Calculate the budget allocation towards the risky assets \(E' = C * M \) and the safe assets \( B' = CPPI - E' \) respectively.
- Compute the new \(CPPI\) value during the time of rebalancing from the assets returns :
$$\begin{align*} CPPI &= E+B \\ &=E'(1+E_{r})+B'(1+B_{r})\end{align*}$$
\(E\) : current risky assets value
\(B\) : current safe assets value
\(E_{r}\) : risky assets returns
\(B_{r}\) : safe assets returns
4. Repeat step-1 & 2 with the new \(CPPI\) value for rebalancing.
*Initially \(CPPI =\) initial investment, then it will take the updated values
Implementation
Let’s consider an investor who wants to invest $100 worth in a CPPI product which consists of risky assets of value \(E\) and safe (riskless) assets of value \(B\). The investor also decides to set the risky assets multiplier \(M\) as 3 based on his analysis and he doesn’t want to lose more than 80% of his initial investment i.e. go below $80. Based on the above information and constraints given by the investor we can construct a CPPI product/portfolio with the steps mentioned previously.
- We calculate the cushion \(C\) :
$$
\begin{align*}
C &= CPPI - F \\
&= 100 -80 \\
&= 20
\end{align*}
$$
We have a cushion of $20.
2. Now we get budget allocation towards the risky assets \(E'\) and safe assets \(B'\):
$$
\begin{align*}
E' &= C * M \\
&= 20 * 3 \\
&= 60
\end{align*}
$$
$$
\begin{align*}
B' &= CPPI - E' \\
&= 100 - 60 \\
&= 40
\end{align*}
$$
Now, we just need to hold $60 worth of risky assets and $40 worth of safe assets to maintain the CPPI portfolio.
3. During rebalancing, we compute the new value of \(CPPI\) :
$$CPPI = E + B$$
Let’s assume our risky asset has done well recently and its value \(E\) increased from $60 to $70, therefore increasing our \(CPPI\) value from $100 to $110 (assuming the safe asset value \(B\) didn’t change). As per the above equation, the calculation will look something like this -
$$CPPI = 70 + 40 = 110$$
4. Now we just need to repeat steps 1 & 2 to get the new allocations :
$$C = 110-80 = 30 \\ E' = 30*3 = 90 \\ B' = 110-90 = 20$$
So, now we have our new allocation for rebalancing, so we increase our risky assets holding by $30 (90 - 60) and decreasing the safe assets holding by $20 (20 - 40).
If the investor ensures doing the rebalancing frequently, it guarantees him that the investments will never breach the floor. But the risk the investor possesses is the GAP risk that can occur due to low rebalancing frequency, in scenarios where the risky asset experiences a huge and sudden fall (which is rare). The GAP risk can be measured by GAP size \(1/M\) , which is the maximum loss that could be sustained between two rebalancing dates before the portfolio breaks the floor. In the above investor’s case, he has a GAP risk of (⅓) = 33.33%, if the risky assets fall below 33.33% between the rebalancing date, \(CPPI\) will breach the floor. Therefore, the higher the value of the multiplier \(M\) , the greater the risk of breaching the floor.
The backtest performance of the above CPPI product/portfolio, when the risky asset is SPY and the safe asset is just cash i.e. it receives a risk-free rate of 4% p.a., is shown as Exhibit-1.
Drawdown Constraint
From the above algorithm, the one thing we can notice is the floor of the CPPI, which is constant throughout. By now it may seem absurd to you that while the portfolio reaches a new height/peak, the chance of breaking the initial floor reduces and we end fully investing in risky assets. Not very attractive, we don’t want to simply protect our investment but also want to secure some profit/growth. Well, by now you might have thought that how about updating our floor as we reach a new high/peak and yes it does make sense. From the previous, investor’s example when the CPPI value raised to $110, we can re-compute the floor i.e. (0.8 * 110) = $88. In other words, now we consider the floor as the maximum drawdown that the investor can suffer (if there is no GAP risk).
To implement the CPPI algorithm with maximum drawdown constraint, we just need to update the re-compute floor before calculating the cushion (consider it as step-0) and the rest of the algorithm remains unchanged. The new floor value is only considered if it is greater than the previous floor value, else the floor remains unchanged. As we can see below, it under performs slightly on returns but significantly better on the risk and drawdown side compared to a normal CPPI and in reality, too no one really uses a plain CPPI without any drawdown constraint.
The above backtests (exhibit-1 &2) are conducted on daily bars of SPY from '2015-01-02' to '2020-12-31' using the run_cppi() function with daily rebalancing in the notebook. Also, the run_cppi() function is used for the backtests.
Trading Algorithm
Perhaps you are impressed by the simplicity of the CPPI algorithm and perhaps considering to live trade it. Thinking the same, I have decided to develop a CPPI strategy with the drawdown constraint for live trading with Alpaca API. But to trade it, you first need to define a few CPPI parameters like - the risky asset you want to invest in, a safe asset if you have one else it keeps the safe allocation as cash in the trading account, the initial investment capital, the floor percentage, the multiplier/leverage and the rebalancing frequency. If you are not sure what parameters to choose, I recommend playing with the parameters in the backtesting notebook to better understand the working.
class CPPI:
"""
The CPPI algorithm class.
"""
def __init__(self, risky_asset:str, cppi_budget:int,
safe_asset:str=None, floor_percent:float=0.8,
asset_muliplier:int=3):
"""
:param assets :(str) the ticker symbols of the risky assets to
invest in. E.g. : 'AAPL' or 'GS'
:param cppi_budget :(int) the budget to be allocated to CPPI
algorithm.
:param safe_asset :(str) the safe asset ticker symbol. Default is
None and will keep the safe allocation as cash
in the trading account.
:param floor_percent :(float) this will be the floor percentage
that the CPPI will try to maintain. Default
is 80% of the initial budget.
:param asset_muliplier :(int) the risky asset multiplier for the
CPPI. This is the risk aversion parameter
and usually it is set between 3 and 6.
Default is 3.
"""
#set the CPPI strategy params
self.risky_asset = risky_asset
self.safe_asset = safe_asset
self.cppi_value = cppi_budget
self.floor_percent = floor_percent
self.floor_value = cppi_budget * floor_percent
self.m = asset_muliplier
self.max_cppi_value = cppi_budget
self.position_value = None
#check if the account permits the given budget
self._check_budget(cppi_budget)
#open a csv file to store the cppi metrics
self.savefile = f'{risky_asset}_cppi.csv'
if not os.path.exists(self.savefile):
with open(self.savefile, 'w', newline='') as file:
wr = csv.writer(file)
#initialize the header
header = ['cppi value', 'floor']
wr.writerow(header)
def _check_budget(self, required_capital:float):
"""
A function that checks if the current account value
meets the CPPI budget.
"""
available_cash = float(api.get_account().cash)
if required_capital > available_cash:
raise Exception("Not enough available cash")Once you have all the parameters that satisfy your analysis, you can start by initializing those parameters to the CPPI class. Before creating an instance it will first check if the given CPPI budget is available as cash in the user's account to trade.
def run(self, period_in_days:int=1):
"""
Start the CPPI algorithm.
:param period_in_days :(int) rebalancing period in days.
Default is 1 day.
"""
self._check_market_open()
#check if any positions already exists for the risky asset
_, _ = self._check_position()
while True:
self.max_cppi_value = max(self.max_cppi_value, self.cppi_value)
self.floor_value = self.max_cppi_value*self.floor_percent
#calculate the cushion
cushion = self.cppi_value - self.floor_value
#compute the allocations towards safe and risky assets
risk_alloc = max(min(self.m*cushion, self.cppi_value), 0)
safe_alloc = self.cppi_value - risk_alloc
#order the allocation
self.rebalance(risk_alloc, safe_alloc)
#sleep till next rebalancing.
time.sleep(period_in_days*24*60*60)
self._check_market_open()
#re-calculate the CPPI value based on the asset holding returns
risky_ret, safe_ret = self._check_position()
self.cppi_value = risk_alloc*(1 + risky_ret) + safe_alloc*
(1 + safe_ret)
#save the tracking metrics
self.save_cppi_metrics()The run() is the main function that runs the CPPI trading algorithm and it takes the rebalancing period (in days) as the only parameter. It checks if any position exists in the risky and safe asset already with _check_position() function and considers that in the CPPI allocation calculation. The main event loop is activated with the algorithm for CPPI with the drawdown constraint (from step-0 to 2 as mentioned above). The allocations are then passed to the rebalance() function which rebalances the position by placing an order to adjust the dollar value of a position using place_order() function to the CPPI allocations.
def place_order(self, symbol:str, dollar_amount:float):
"""
A function that places a market order in Alpaca based on the
dollar amount to buy (e.g. $1000) or short (e.g. -$1000)
for the given asset symbol.
"""
if np.sign(dollar_amount) > 0:
side = 'buy'
elif np.sign(dollar_amount) < 0:
side = 'sell'
current_asset_price = api.get_last_trade(symbol).price
qty = int(abs(dollar_amount) / current_asset_price)
if qty > 0:
order = api.submit_order(symbol=symbol,
qty=qty,
side=side,
type='market',
time_in_force='day')
def rebalance(self, risk_alloc:float, safe_alloc:float):
"""
This function will check if any rebalancing is required based on the
recent CPPI risk budget allocation.
"""
if self.position_value is None:
#long the entire budget
self.place_order(self.risky_asset, risk_alloc)
#buy the safe asset also if given
if self.safe_asset is not None:
self.place_order(self.safe_asset, safe_alloc)
else:
#get the excess risk allocation
excess_risk_alloc = risk_alloc - self.position_value[0]
excess_safe_alloc = safe_alloc - self.position_value[1]
#check if rebalancing is required
if abs(excess_risk_alloc) > 0:
#rebalance the risky asset
self.place_order(self.risky_asset, excess_risk_alloc)
#rebalance the safe asset if available
if self.safe_asset is not None:
self.place_order(self.safe_asset, excess_safe_alloc)Then the algorithm sleeps till the next rebalancing when it first checks if the market is open, then it re-calculates the CPPI value base on the current returns on the positions for the risk and safe asset both acquired from _check_position() function (step-4).
def _check_position(self):
"""
A function to retrieve the current position value and return of
risky and safe assets.
"""
risky_position, risky_ret = self.get_position_value(self.risky_asset)
if risky_position is not None:
if self.safe_asset is not None:
safe_position,safe_ret = self.get_position_value(self.safe_asset)
if safe_position is not None:
#both position exists
self.position_value = [risky_position, safe_position]
else:
#safe asset position doesn't exists
self.position_value = [risky_position, 0]
safe_ret = 0
elif self.safe_asset is not None:
safe_position,safe_ret = self.get_position_value(self.safe_asset)
if safe_position is not None:
#only safe asset position exists
self.position_value = [0, safe_position]
risk_ret = 0
else:
#no position exists for either
self.position_value = None
risky_ret = 0
return risky_ret, safe_ret
def save_cppi_metrics(self):
with open(savefile, 'w', newline='') as file:
wr = csv.writer(file)
wr.writerow([self.cppi_value, self.floor_value])Finally, we save the CPPI value and the floor value in a CSV file for later post-trade analysis using the save_cppi_metrics() and rebalance the current position using the allocations calculated from the new CPPI value.
Running Strategy Instance
Once you find your desired strategy parameters it is straight forward and simple to run an instance of the strategy. Below example runs an instance of CPPI with SPY as the risky asset and considering cash as the safe asset since None is given. Also, it allocates $1000 towards the CPPI and daily rebalancing frequency, a floor of 80% and multiplier as 3.
#set the strategy params
r_asset = 'SPY'#risky_asset
s_asset = None #safe_asset
capital = 1000
rebalance_freq = 1 #days or daily
floor_pct = 0.8 #80%
m = 3 #asset_muliplier
#create a instance
spy_cppi = CPPI(risky_asset=r_asset, cppi_budget=capital, safe_asset=s_asset,
floor_percent=floor_pct, asset_muliplier=m)
#start the strategy
spy_cppi.run(period_in_days=reblance_freq)Conclusion
In this article, I have explained the concept of portfolio insurance with the help of CPPI, a simple yet effective strategy for downside protection without hedging or involving derivatives. A vanilla CPPI algorithm can perform much better with a drawdown constraint that updates the floor along the way. So, it is not very practical to implement a CPPI trading strategy without the drawdown constraint. The investors must carefully choose the multiplier \(M\) and rebalance it frequently by considering the transaction cost and commissions. With decreasing transaction costs, CPPI style strategies are becoming practical and algorithmic trading makes frequent rebalancing possible and effortless.
We have touched the basics here, CPPI can be used in many variations and can be combined with existing portfolio strategies to gain the most out of it. An example of trading a portfolio (FAANG) with CPPI is shown in the notebook.
Reference Links
To understand this article better I recommend you the following resources:
- http://www.deltaquants.com/Introduction-to-risks-in-CPPI-products
- https://medium.com/swlh/protect-your-portfolio-using-cppi-strategy-in-python-c3184c2b6767
- https://www.coursera.org/lecture/introduction-portfolio-construction-python/an-introduction-to-cppi-part-1-TYWck
- https://risk.edhec.edu/publications/growth-optimal-portfolio-insurance-long-term
This project’s Github Repository: https://github.com/Harkishan-99/Alpaca-CPPI
You can also follow Alpaca and our weekly updates on our LinkedIn, Alpaca Community Slack and @AlpacaHQ on Twitter!
Brokerage services are provided by Alpaca Securities LLC ("Alpaca"), memberFINRA/SIPC, a wholly-owned subsidiary of AlpacaDB, Inc. Technology and services are offered by AlpacaDB, Inc.




