The options wheel strategy is a popular and versatile approach in options trading, offering investors a structured way to potentially generate premium income while properly managing risk. In this guide, we will cover: what the wheel strategy is, the steps involved in executing this strategy, some of the key concepts, and how to start building this trading strategy algorithmically using Alpaca’s Trading API.
What is the Wheel Strategy in Options?
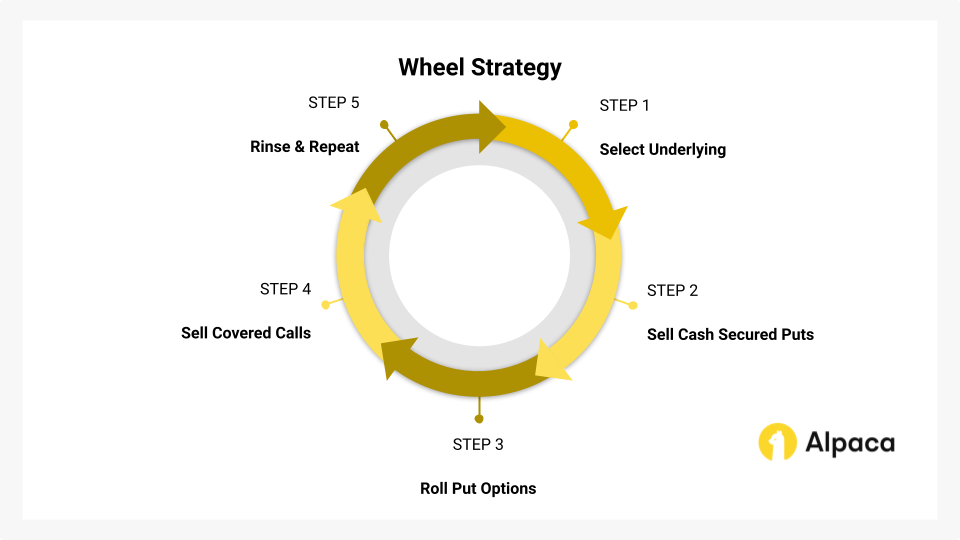
The wheel strategy is a popular options trading approach that combines selling cash-secured puts and covered calls to generate income with the potential for long-term stock ownership. It's a cyclical process requiring active management and understanding of the underlying asset.
Step 1: Select the Underlying Asset
The success of the wheel strategy hinges on selecting an appropriate stock or ETF. While high premiums might be tempting, it's crucial to prioritize underlying assets that align with your investment goals. Consider these assets as potential additions to your portfolio, rather than solely focusing on short-term option premiums.
Some things to consider when selecting the underlying asset:
- You are comfortable owning for the long term.
- Fit your capital constraints, ensuring you can afford to buy 100 shares (or one options contract).
- Have steady, reliable performance with moderate volatility.
Remember, the foundation of a wheel strategy lies in choosing an underlying asset that balances potential returns with your overall risk tolerance and investment objectives.
Step 2: Sell Cash-Secured Puts
The wheel strategy initiates with selling cash-secured puts (CSPs). By selling a CSP, you can potentially generate premium income while establishing a defined entry point for acquiring the underlying stock. Essentially, you're selling the right to sell you the stock at the strike price before the expiration date.
If the option buyer exercises their right to sell you the stock, because the market price is below the strike price, you're obligated to purchase it. However, the premium you received for selling the put can potentially offset this cost.
The CSP strategy offers a dual potential for profit. The first is that the stock price remains above the strike price at expiration, meaning you keep the premium and the option expires worthless. The second is that the stock price falls below the strike price and the option is exercised. You then would buy the stock at the strike price, but the premium you received reduces your effective cost basis.
It's essential to note that while a CSP may be sold at any strike price, strategic selection is crucial. The chosen strike price should typically align with a price level at which the trader is genuinely comfortable owning the underlying stock. This ensures that potential assignment aligns with the trader's investment thesis, rather than being driven solely by the pursuit of option premium.
Step 3: Put Option Roll Management (Optional)
Rolling a put option is a proactive risk management strategy within the wheel strategy. If the underlying stock's price nears or drops below the strike price of your short put, rolling the option can potentially help mitigate losses and generate additional premium income.
How to Roll a Put Option:
- Close the Current Position: Buy back the existing short put option.
- Open a New Position: Simultaneously sell a new put option with adjusted parameters.
- Expiration Date: The new option's expiration date is usually further out in time. This is referred to as "rolling out."
- Strike Price: The strike price is often adjusted higher, closer to the current underlying stock price. This is known as "rolling up."
The goal is to execute the roll for a net credit. This means the premium received from selling the new put should typically exceed the cost of closing the original position. If the put is assigned, this net credit reduces your overall cost basis for the underlying stock. If the put expires out-of-the-money (OTM), the net credit increases your total premium income.
Below is the profit/loss diagram of the wheel strategy where you see the following three points:
- Maximum Profit Point: when the strike price of the covered call (CC) is higher than (strike price of CSP + premiums for both approaches).
- Break Even Point: when the strike price of the CC is equal to (strike price of CSP + premiums for both approaches).
- Maximum Loss Point: when the strike price of the CC is less than (strike price of CSP + premiums for both approaches).
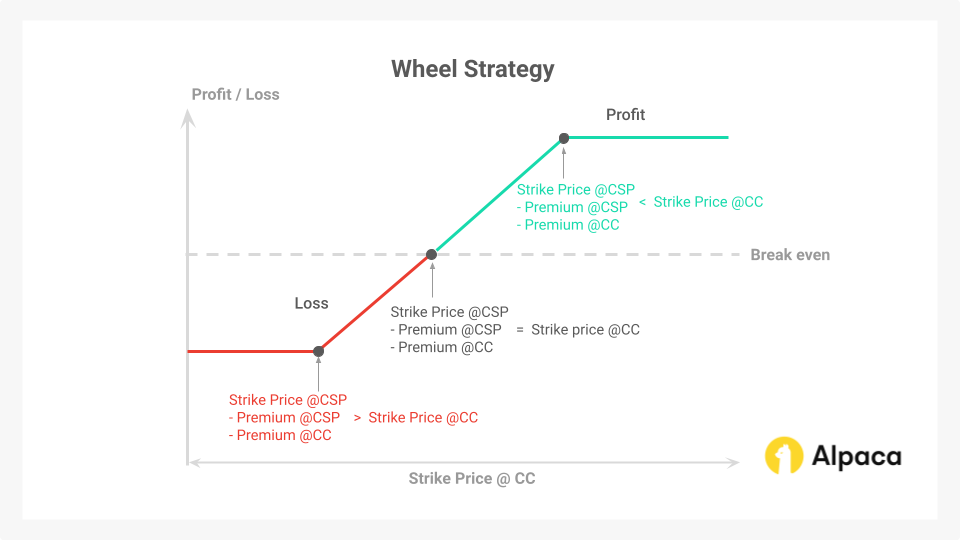
Note: this does not illustrate the potential opportunity cost if the underlying asset’s price rises significantly above the strike price. It also doesn't show the potential for increased losses if the price drops substantially below the strike price of the cash-secured put (CSP).
Step 4: Covered Call Implementation
After the put option is assigned in Step 2, the wheel strategy transitions to a covered call (CC) position. This involves selling a call option against the 100 shares of the acquired stock. The CC can potentially generate additional premium income, while capping potential upside profit. You can think of the CC premium as "rental income" earned on the owned stock.
Covered Call Mechanics:
- Premium Collection: You (the seller) receive a premium upfront by selling the call option.
- Profit Scenario: If the stock price stays below the strike price at expiration, the seller keeps the premium and retains the shares.
- Assignment Scenario: If the stock price exceeds the strike price, the shares are called away (sold) at the strike price.
Strike Price Selection:
- Profit Target: The strike price is typically chosen at or above a predetermined profit target for the underlying stock. This allows the trader to lock in gains if the stock appreciates.
- Delta (0.20 to 0.40): Picking a moderate delta range may potentially balance premium income with the probability of assignment.
Step 5: Iteration and Portfolio Management
As the name suggests, the wheel strategy is cyclical. When shares are sold, either through call assignment or a separate decision, the process returns to Step 2.
This involves identifying a new underlying asset or re-evaluating the original one, then selling cash-secured puts to initiate a new wheel "spin." This cyclical nature allows for consistent income generation.
However, it's crucial to emphasize that this strategy demands active management. The wheel strategy’s success lies not in a single trade but in its disciplined, repeatable execution over time, which is why algotrading can be so beneficial in trading this strategy.
Key Concepts and Considerations
The wheel strategy's effectiveness hinges on a solid understanding of the option Greeks, the mathematical parameters that influence option pricing.
Option Greeks
Delta
Delta is a critical concept in options trading, representing an option's price sensitivity to changes in the underlying asset's price. It also serves as a helpful indicator of the probability that the option will expire "in-the-money" (ITM).
For example, a put option with a delta of -0.40 suggests a 40% chance of being exercised (assigned). In the options wheel strategy, delta is used to strategically select options that balance premium income with the desired level of risk.
Theta
Theta, a measure of time decay, quantifies how an option's value erodes as its expiration date approaches. This decay is non-linear, accelerating significantly as the option nears expiry. Wheel traders, who primarily sell options, can leverage this time decay to their advantage.
However, it's crucial to be mindful of the risks associated with short-dated options. From 30 days to expiration (DTE) to 0DTE, theta decay intensifies, increasing the potential for sharp price movements in the underlying stock to impact the trade. Such volatility can potentially disrupt the wheel strategy's income-generating objective.
Vega
Vega gauges an option's price sensitivity to changes in implied volatility (IV) — the market's forecast of future price fluctuations in the underlying asset. A 1% shift in IV corresponds to a change in the option's price equal to its vega value.
Importantly, vega is independent of both time decay and the underlying stock's price. While high-IV options may offer enticing premiums, they also come with increased risk due to the potential for significant price swings. This trade-off necessitates a cautious approach and diligent risk management.
Risk Management
Effective risk management is at the core of any trading strategy, and the wheel strategy is no exception. A key requirement is the use of cash-secured puts, meaning you must have enough capital available to purchase the underlying shares if assigned. By ensuring you can cover the cost of assignment, you mitigate the risk of forced liquidation and maintain control over your positions. Remember, assignment is not a failure in the wheel strategy; it's a planned scenario that can lead to acquiring the underlying asset at a favorable price.
Also, it’s typically a best practice to avoid overleveraging by sizing positions appropriately and only trading what your account can comfortably handle. Setting stop-loss orders may provide an additional safety net to limit unexpected losses. One possible risk management strategy is to set the risk of each trade as 1-2% of your total account balance. For example, if your account is $50,000, aim to risk no more than $500 to $1,000 for the covered call.
How to Trade the Wheel Strategy (Alpaca’s Trading API Examples)
This section provides a detailed walkthrough of implementing the wheel strategy using Python and Alpaca’s Trading API and Alpaca’s Paper Trading. Remember that the strategy involves selling CSPs to acquire stock, selling CCs on assigned shares, and repeating the process. This example implementation uses key metrics and filters to streamline decision-making and manage risk effectively. If you’re not connected to Alpaca’s API, learn how to start paper trading with Alpaca.
Note: The code outlined below assumes a flat interest rate, does not consider dividends, is not optimized for 0DTE options, and does not consider whether the market is open or closed. The below code should only be considered a starting point to creating a wheel strategy, not a finished strategy.
(Please note that we are using the stock “WMT” as an example and it should not be considered investment advice.)
Step 1: Setting Up the Environment
Before diving into the wheel strategy, we need to set up the programming environment. Below is the initial code block for configuring the variables that will be used throughout the demonstration.
First, install and import the necessary packages and libraries, including `alpaca-py,` and specify your Alpaca Paper Trading API keys. This allows you to initialize the Alpaca clients which will be used to execute the wheel strategy.
# Install the alpaca-py first
! python3 -m pip install alpaca-py
import pandas as pd
import numpy as np
from scipy.stats import norm
import alpaca
import time
from scipy.optimize import brentq
from datetime import datetime, timedelta
from zoneinfo import ZoneInfo
from alpaca.data.timeframe import TimeFrame, TimeFrameUnit
import os
from alpaca.trading.client import TradingClient
from alpaca.data.historical.option import OptionHistoricalDataClient
from alpaca.data.historical.stock import StockHistoricalDataClient, StockLatestTradeRequest
from alpaca.data.requests import StockBarsRequest, OptionLatestQuoteRequest, OptionChainRequest
from alpaca.trading.requests import GetOptionContractsRequest, MarketOrderRequest
from alpaca.trading.enums import AssetStatus, ContractType
# API credentials for Alpaca
API_KEY = "YOUR_ALPACA_API_KEY_FOR_PAPER_TRADING"
API_SECRET = 'YOUR_ALPACA_API_SECRET_KEY_FOR_PAPER_TRADING'
BASE_URL = None
## We use paper environment for this example
PAPER = True # Please do not modify this. This example is for paper trading only.
# Initialize Alpaca clients
trade_client = TradingClient(api_key=API_KEY, secret_key=API_SECRET, paper=PAPER, url_override=BASE_URL)
option_historical_data_client = OptionHistoricalDataClient(api_key=API_KEY, secret_key=API_SECRET, url_override=BASE_URL)
stock_data_client = StockHistoricalDataClient(api_key=API_KEY, secret_key=API_SECRET)
# Below are the variables for development this documents
# Please do not change these variables
trade_api_url = None
trade_api_wss = None
data_api_url = None
option_stream_data_wss = NoneWe also define several key variables to streamline later operations:
underlying_symbol: The stock symbol for the underlying asset (e.g., 'WMT' for Walmart).STRIKE_RANGE: Sets a ±10% range around the current stock price for selecting strike prices.BUY_POWER_LIMIT: Caps the buying power allocation for CSPs to 10% of the account value.RISK_FREE_RATE: Assumes a 1% rate for calculating option Greeks.OI_THRESHOLD: Sets a minimum open interest threshold (e.g., 200 contracts) for liquidity.Expiration Date Range: Filters options expiring between 14 and 35 days.Strike Price Range: Sets the options strike prices range within a 5% range around the underlying price
# Configuration
underlying_symbol = 'WMT'
# Set expiration range for options
today = datetime.now().date()
# Define a 5% range around the underlying price
STRIKE_RANGE = 0.05
# Buying power percentage to use for the trade
BUY_POWER_LIMIT = 0.10
# Risk free rate for the options greeks and IV calculations
RISK_FREE_RATE = 0.01
# Check account buying power
buying_power = float(trade_client.get_account().buying_power)
# Calculate the limit amount of buying power to use for the trade
buying_power_limit = buying_power * BUY_POWER_LIMIT
# Set the open interest volume threshold
OI_THRESHOLD = 200
# Set the expiration date range for the options
min_expiration = today + timedelta(days=4)
max_expiration = today + timedelta(days=35)
# Get the latest price of the underlying stock
def get_underlying_price(symbol):
# Get the latest trade for the underlying stock
underlying_trade_request = StockLatestTradeRequest(symbol_or_symbols=symbol)
underlying_trade_response = stock_data_client.get_stock_latest_trade(underlying_trade_request)
return underlying_trade_response[symbol].price
# Get the latest price of the underlying stock
underlying_price = get_underlying_price(underlying_symbol)
print(f"{underlying_symbol} price: {underlying_price}")
# Set the minimum and maximum strike prices based on the underlying price
min_strike = str(underlying_price * (1 - STRIKE_RANGE))
max_strike = str(underlying_price * (1 + STRIKE_RANGE))
# Display the values
print(f"Underlying Symbol: {underlying_symbol}")
print(f"Today's Date: {today}")
print(f"Strike Range: {STRIKE_RANGE}")
print(f"Buying Power Limit Percentage: {BUY_POWER_LIMIT}")
print(f"Risk Free Rate: {RISK_FREE_RATE}")
print(f"Account Buying Power: {buying_power}")
print(f"Buying Power Limit: {buying_power_limit}")
print(f"Open Interest Threshold: {OI_THRESHOLD}")
print(f"Minimum Expiration Date: {min_expiration}")
print(f"Maximum Expiration Date: {max_expiration}")
print(f"Minimum Strike Price: {min_strike}")
print(f"Maximum Strike Price: {max_strike}")In addition to configuration settings, we define a function called calculate_implied_volatility to calculate implied volatility (IV) and a function called calculate_delta to calculate the key option Greek, such as delta. These functions utilize Black-Scholes model to calculate the theoretical IVs and option Greeks. The function takes inputs such as option price, strike price, expiration date, underlying price, risk-free rate, and option type.
These calculations allow for more informed decision-making when selecting appropriate options for both the cash-secured put and covered call strategies. By integrating these functions, traders and developers can automate critical aspects of options analysis, ensuring accuracy and efficiency in strategy execution.
# Calculate implied volatility
def calculate_implied_volatility(option_price, S, K, T, r, option_type):
# Define a reasonable range for sigma
sigma_lower = 1e-6
sigma_upper = 5.0 # Adjust upper limit if necessary
# Check if the option is out-of-the-money and price is close to zero
intrinsic_value = max(0, (S - K) if option_type == 'call' else (K - S))
if option_price <= intrinsic_value + 1e-6:
# print("Option price is close to intrinsic value; implied volatility is near zero.") # Uncomment for checking the status
return 0.0
# Define the function to find the root
def option_price_diff(sigma):
d1 = (np.log(S / K) + (r + 0.5 * sigma ** 2) * T) / (sigma * np.sqrt(T))
d2 = d1 - sigma * np.sqrt(T)
if option_type == 'call':
price = S * norm.cdf(d1) - K * np.exp(-r * T) * norm.cdf(d2)
elif option_type == 'put':
price = K * np.exp(-r * T) * norm.cdf(-d2) - S * norm.cdf(-d1)
return price - option_price
try:
return brentq(option_price_diff, sigma_lower, sigma_upper)
except ValueError as e:
print(f"Failed to find implied volatility: {e}")
return None
# Calculate option Delta
def calculate_delta(option_price, strike_price, expiry, underlying_price, RISK_FREE_RATE, option_type):
T = (expiry - pd.Timestamp.now()).days / 365
T = max(T, 1e-6) # Set minimum T to avoid zero
if T == 1e-6:
print("Option has expired or is expiring now; setting delta based on intrinsic value.")
if option_type == 'put':
return -1.0 if underlying_price < strike_price else 0.0
else:
return 1.0 if underlying_price > strike_price else 0.0
implied_volatility = calculate_implied_volatility(option_price, underlying_price, strike_price, T, RISK_FREE_RATE, option_type)
print(f"implied volatility is {implied_volatility}")
if implied_volatility is None or implied_volatility == 0.0:
print("Implied volatility could not be determined, skipping delta calculation.")
return None
d1 = (np.log(underlying_price / strike_price) + (RISK_FREE_RATE + 0.5 * implied_volatility ** 2) * T) / (implied_volatility * np.sqrt(T))
delta = norm.cdf(d1) if option_type == 'call' else -norm.cdf(-d1)
return deltaStep 2: Select the Underlying Asset
Selecting the right underlying stock is foundational for the wheel strategy. The code uses Average True Range (ATR) to gauge the stock's price volatility. ATR measures the average price movement over a specified period, helping traders identify stocks that strike a balance between risk and reward. The function get_atr_for_stock calculates a 14-day ATR over the past 90 days, ensuring the underlying aligns with your volatility criteria.
While not explicitly implemented in the code below, the Relative Strength Index (RSI) is a valuable tool for identifying overbought and oversold conditions. RSI is a momentum oscillator that ranges from 0 to 100. These indicators help traders identify stocks that strike a balance between risk and reward. For the wheel strategy, an example RSI range could be between 20 and 80 to avoid extreme market conditions.
# Calculate ATR for the underlying stock
# Get the historical data for the underlying stock by symbol
# ref. https://docs.alpaca.markets/reference/stockbars-1
def get_stock_data(underlying_symbol, stock_data_client, days=90):
now = datetime.now(ZoneInfo("America/New_York"))
req = StockBarsRequest(
symbol_or_symbols=[underlying_symbol],
timeframe=TimeFrame(amount=1, unit=TimeFrameUnit.Day), # specify timeframe
start=now - timedelta(days=days), # specify start datetime, default=the beginning of the current day.
)
return stock_data_client.get_stock_bars(req).df
# Calculate True Range for the underlying stock in the last 90 days
def calculate_true_range(data):
data['prev_close'] = data['close'].shift(1) # Shift the closing price by 1 day
data['tr'] = np.maximum(
data['high'] - data['low'],
np.maximum(
abs(data['high'] - data['prev_close']),
abs(data['low'] - data['prev_close'])
)
)
return data
# Calculate ATR for the underlying stock on the last 90 days
def calculate_atr(data, period=14):
data['atr'] = data['tr'].rolling(window=period).mean()
return data
def get_atr_for_stock(underlying_symbol, period=14):
data = get_stock_data(underlying_symbol, stock_data_client, days=90)
data = calculate_true_range(data)
data = calculate_atr(data, period=period)
return data[['tr', 'atr']].dropna() # Return only TR and ATR columns
# Calculate 14-day Average True Ranges (ATRs) over 90 days
results = get_atr_for_stock(underlying_symbol=underlying_symbol, period=14)
atr_mean_90 = results["atr"].mean()
print(f"14-day ATR over 90 days is: {atr_mean_90}")Step 3: Sell Cash-Secured Puts
Selling CSPs allows traders to potentially generate income while preparing to purchase the stock at a desired price. The code filters for suitable CSPs using key metrics and criteria.
One of the common mistakes traders make in the wheel strategy is trading underlying stocks they may not actually want to own. While there’s no perfect stock for the wheel strategy, it’s crucial to emphasize that traders generally only use this strategy with stocks they are willing to own and have the capital to purchase 100 shares.
Key Elements for Filtering CSP Options:
- Delta (-0.20 to -0.40): Balances premium collection with the probability of assignment.
- Open Interest Volume Threshold (500): Ensures adequate liquidity for smoother execution.
- Buying Power Limit (10%): Restricts capital usage to avoid overleveraging.
- DTE (14–35 days): Targets options within this expiration range for optimal time decay and risk management.
The get_put_options function retrieves put options for the assigned stock. It filters options based on strike price and expiration date, ensuring they meet criteria such as:
- Strike prices starting from the minimum strike price up to an upper limit.
- Expiration dates falling within 14 to 35 days.
# Check for put options
def get_put_options(underlying_symbol, min_strike, max_strike, min_expiration, max_expiration):
# Fetch the options data to add to the portfolio
req = GetOptionContractsRequest(underlying_symbols=[underlying_symbol],
strike_price_gte=min_strike,
strike_price_lte=max_strike,
status=AssetStatus.ACTIVE,
expiration_date_gte=min_expiration,
expiration_date_lte=max_expiration,
root_symbol=underlying_symbol,
type=ContractType.PUT,
)
# Get put option chain of the underlying symbol
put_options = trade_client.get_option_contracts(req).option_contracts
return put_optionsOnce the options are retrieved, the find_short_put_option function evaluates them to select the best one. It calculates the delta for each option and applies the following filters:
- Delta: Between -0.40 and -0.20 to balance premium collection with assignment risk.
- Buying Power Limit: The total contract cost is below the buying power limit.
# Find the appropriate short put option to sell based on the delta and buying power limit
def find_short_put_option(put_options, underlying_price, RISK_FREE_RATE, buying_power_limit):
short_put = None
for option_data in put_options:
try:
# Ensure open_interest is valid and open_interest_date exists
if option_data.open_interest is None or option_data.open_interest_date is None:
# Skip options with missing open interest or quote data
continue
# Check open interest meets the threshold
if float(option_data.open_interest) <= OI_THRESHOLD:
print(f"Skipping option {option_data.symbol} due to lack of open interest. You may change the OI_THRESHOLD") # Uncomment for checking the status
continue
# Get the latest quote for the option price
option_symbol = option_data.symbol
option_quote_request = OptionLatestQuoteRequest(symbol_or_symbols=option_symbol)
option_quote = option_historical_data_client.get_option_latest_quote(option_quote_request)[option_symbol]
# Extract option details
option_price = (option_quote.bid_price + option_quote.ask_price) / 2
option_size = float(option_data.size)
strike_price = float(option_data.strike_price)
expiry = pd.Timestamp(option_data.expiration_date)
print(f"option_symbol is {option_symbol}")
print(f"option_price is {option_price}")
print(f"strike price is {strike_price}")
# Calculate delta for each option
delta = calculate_delta(
option_price=option_price,
strike_price=strike_price,
expiry=expiry,
underlying_price=underlying_price,
RISK_FREE_RATE=RISK_FREE_RATE,
option_type='put'
)
print(f"delta is {delta}")
# Check if delta is between -0.42 and -0.18 and if the total contract exceeds the buying power limit
if delta is not None and delta >= -0.42 and delta <= -0.18 and strike_price * option_size < buying_power_limit:
# Create the appropriate short put option in the dictionary format
short_put = {
'close_price': option_data.close_price,
'close_price_date': option_data.close_price_date,
'expiration_date': option_data.expiration_date,
'id': option_data.id,
'name': option_data.name,
'open_interest': option_data.open_interest,
'open_interest_date': option_data.open_interest_date,
'root_symbol': option_data.root_symbol,
'size': option_data.size,
'status': option_data.status,
'strike_price': option_data.strike_price,
'style': option_data.style,
'symbol': option_data.symbol,
'tradable': option_data.tradable,
'type': option_data.type,
'underlying_asset_id': option_data.underlying_asset_id,
'underlying_symbol': option_data.underlying_symbol,
'initial_delta': delta,
'initial_option_price': option_price,
}
print(f"short_put is {short_put}")
# If the short put is found, break the loop
if short_put:
break
except KeyError as e:
print(f"Missing data for option {option_symbol}: {e}")
continue
return short_putThe execute_cash_secured_put function automates the process of placing a cash secured put order. It first retrieves a list of put options for a specified underlying stock and filters them based on criteria such as delta and available buying power. Once a suitable option is found, it places a market order to sell the put, ensuring the trade aligns with the predefined risk and profit thresholds. If no suitable options are found, the function returns an appropriate message.
def execute_cash_secured_put(underlying_symbol, RISK_FREE_RATE, buying_power_limit, min_strike, max_strike, min_expiration, max_expiration):
# Get put options
put_options = get_put_options(underlying_symbol, min_strike, max_strike, min_expiration, max_expiration)
if put_options:
# Get the latest price of the underlying stock
underlying_price = get_underlying_price(symbol=underlying_symbol)
# Find appropriate short put options
short_put = find_short_put_option(put_options, underlying_price, RISK_FREE_RATE=RISK_FREE_RATE, buying_power_limit=buying_power_limit)
# Proceed if short put options are found
if short_put:
# Place orders for the strategy
# Sell the -20 ~ -40 delta put
req = MarketOrderRequest(
symbol=short_put['symbol'],
qty=1,
side='sell',
type='market',
time_in_force='day'
)
trade_client.submit_order(req)
success_message = (f"Placing Cash Secured Put on {underlying_symbol} successfully:\n"
f"Sell {short_put['initial_delta']} Delta Put: {short_put['symbol']} "
f"(Strike: {short_put['strike_price']}, Premium to Receive: {short_put['initial_option_price']})")
return success_message, short_put
else:
return "Could not find suitable options which has delta between -20 and -40.", None
else:
return "No put options available for the underlying symbol.", NoneYou can run the find_short_put_option function just to find the short put option.
put_options = get_put_options(underlying_symbol, min_strike, max_strike, min_expiration, max_expiration)
short_put_list = find_short_put_option(put_options, underlying_price, RISK_FREE_RATE, buying_power_limit)
short_put_listOr run the execute_cash_secured_put function to execute the cash secured put.
message, short_put = execute_cash_secured_put(underlying_symbol, RISK_FREE_RATE, buying_power_limit, min_strike, max_strike, min_expiration, max_expiration)
message, short_putStep 4: Sell Covered Calls (CCs)
Once the stock is assigned, the next step is to sell covered calls to potentially generate additional income. The strike price and delta are critical to ensure profitability and manage upside risk.
Key Elements for Filtering CC Options:
- Delta (0.20 to 0.40): Balances premium collection and the likelihood of being called away.
- Upper Bollinger Band: Ensures the strike price is above significant resistance levels.
- Open Interest Volume Threshold (500): Similar to CSPs, this ensures liquidity.
To determine the optimal strike price for a covered call, the code calculates the Upper Bollinger Band, a resistance level based on historical price data. The band is derived using the following steps:
- Simple Moving Average (SMA): Average closing prices over the past 20 days.
- Standard Deviation (StdDev): Measures price variability over the same period.
- Upper Bollinger Band: Calculated as
SMA + (2 × StdDev).
# setup stock historical data client
now = datetime.now(ZoneInfo("America/New_York"))
req = StockBarsRequest(
symbol_or_symbols = [underlying_symbol],
timeframe=TimeFrame(amount = 1, unit = TimeFrameUnit.Day), # specify timeframe
start = today - timedelta(days = 60), # specify start datetime, default=the beginning of the current day.
end=today, # specify end datetime, default=now
)
stock_data = stock_data_client.get_stock_bars(req).df
# Define the window period for the Bollinger Bands
window = 20
# Calculate the Simple Moving Average (SMA)
stock_data['SMA'] = stock_data['close'].rolling(window=window).mean()
# Calculate the rolling standard deviation
stock_data['StdDev'] = stock_data['close'].rolling(window=window).std()
# Set the multiplier (commonly 2)
multiplier = 2
# Calculate the Upper Bollinger Band
stock_data['Upper Band'] = stock_data['SMA'] + (multiplier * stock_data['StdDev'])
# Get the most recent Upper Band value
latest_upper_bollinger_band = stock_data['Upper Band'].iloc[-1]
print(f"Latest Upper Bollinger Band is: {latest_upper_bollinger_band}")Using the has_sufficient_shares function, you can extract information about your holdings and determine if you have enough shares to execute a covered call. For further details, you can also refer to Alpaca API Documentation.
# Check if the portfolio has sufficient shares of the underlying stock/ETF to execute a covered call
def has_sufficient_shares(symbol, required_qty=100):
# Fetch all positions
positions = trade_client.get_all_positions()
# Iterate through positions to check the stock symbol
for position in positions:
if position.symbol == symbol and position.asset_class == 'us_equity':
# Check if the available quantity is greater than or equal to the required quantity
if int(position.qty_available) >= required_qty:
print(f"Sufficient shares available for {symbol}.")
return True
else:
print(f"Insufficient shares for {symbol}. Required: {required_qty}, Available: {position.qty_available}")
return False
print(f"No position found for the stock: {symbol}")
return False
# If the portfolio has sufficient shares, run the following codes to execute the covered call
has_sufficient_shares(underlying_symbol)The get_call_options function retrieves call options for the assigned stock. It filters options based on strike price and expiration date, ensuring they meet criteria such as:
- Strike prices starting from the CSP’s strike price up to an upper limit.
- Expiration dates falling within 14 to 35 days.
# Check for call options which are above the short_put strike price
def get_call_options(underlying_symbol, option_data, max_strike, min_expiration, max_expiration):
# Check if the purchased option strike (=option_data['strike_price']) in the CSP is less than max_strike
if option_data['strike_price'] >= float(max_strike):
return f"Option with strike price {option_data['strike_price']} exceeds the max strike price {max_strike}."
# Fetch the options data to add to the portfolio
req = GetOptionContractsRequest(underlying_symbols=[underlying_symbol],
strike_price_gte=str(option_data['strike_price']),
strike_price_lte=max_strike,
status=AssetStatus.ACTIVE,
expiration_date_gte=min_expiration,
expiration_date_lte=max_expiration,
root_symbol=underlying_symbol,
type=ContractType.CALL,
)
# Get put option chain of the underlying symbol
call_options = trade_client.get_option_contracts(req).option_contracts
return call_optionsOnce the options are retrieved, the find_short_call_option function evaluates them to select the best one. It calculates the delta for each option and applies the following filters:
- Delta: Between 0.20 and 0.40 to balance premium collection with assignment risk.
- Strike Price: Above the upper Bollinger Band to ensure the strike price exceeds a key resistance level.
# Find the appropriate short call option to sell based on the delta and buying power limit
def find_short_call_option(call_options, underlying_price, RISK_FREE_RATE, latest_upper_bollinger_band):
short_call = None
for option_data in call_options:
try:
# Ensure open_interest is valid and open_interest_date exists
if option_data.open_interest is None or option_data.open_interest_date is None:
# Skip options with missing open interest or quote data
continue
# Check open interest meets the threshold
if float(option_data.open_interest) <= OI_THRESHOLD:
# print(f"Skipping option {option_name} due to missing trade or quote data.") # Uncomment for checking the status
continue
# Get the latest quote for the option price
option_symbol = option_data.symbol
option_quote_request = OptionLatestQuoteRequest(symbol_or_symbols=option_symbol)
option_quote = option_historical_data_client.get_option_latest_quote(option_quote_request)[option_symbol]
# Extract option details
option_price = (option_quote.bid_price + option_quote.ask_price) / 2
option_size = float(option_data.size)
strike_price = float(option_data.strike_price)
expiry = pd.Timestamp(option_data.expiration_date)
print(f"option_symbol is {option_symbol}")
print(f"option_price is {option_price}")
print(f"strike price is {strike_price}")
# Calculate delta for each option
delta = calculate_delta(
option_price=option_price,
strike_price=strike_price,
expiry=expiry,
underlying_price=underlying_price,
RISK_FREE_RATE=RISK_FREE_RATE,
option_type='call'
)
print(f"delta is {delta}")
# Check if delta is between 0.42 and 0.18 and if the strike price is greater than the latest upper boiler band
if delta is not None and delta >= 0.18 and delta <= 0.42 and strike_price > latest_upper_bollinger_band:
# Create the appropriate short put option in the dictionary format
short_call = {
'close_price': option_data.close_price,
'close_price_date': option_data.close_price_date,
'expiration_date': option_data.expiration_date,
'id': option_data.id,
'name': option_data.name,
'open_interest': option_data.open_interest,
'open_interest_date': option_data.open_interest_date,
'root_symbol': option_data.root_symbol,
'size': option_data.size,
'status': option_data.status,
'strike_price': option_data.strike_price,
'style': option_data.style,
'symbol': option_data.symbol,
'tradable': option_data.tradable,
'type': option_data.type,
'underlying_asset_id': option_data.underlying_asset_id,
'underlying_symbol': option_data.underlying_symbol,
'initial_delta': delta,
'initial_option_price': option_price,
}
print(f"short_call is {short_put}")
# If the short put is found, break the loop
if short_call:
break
except KeyError as e:
print(f"Missing data for option {option_symbol}: {e}")
continue
return short_callThis function executes a covered call only if sufficient shares (qty=100) of underlying stock/ETF are available.
def execute_covered_call(underlying_symbol, RISK_FREE_RATE, latest_upper_bollinger_band, option_data, max_strike, min_expiration, max_expiration):
"""
Execute a covered call strategy if sufficient shares are available.
"""
required_qty = 100
if not has_sufficient_shares(underlying_symbol, required_qty):
return f"Insufficient shares for {underlying_symbol} to execute a covered call.", None
# Get call options
call_options = get_call_options(underlying_symbol, option_data, max_strike, min_expiration, max_expiration)
if call_options:
# Get the latest price of the underlying stock
underlying_price = get_underlying_price(symbol=underlying_symbol)
# Find appropriate short put options
short_call = find_short_call_option(call_options, underlying_price, RISK_FREE_RATE, latest_upper_bollinger_band)
# Proceed if short call options are found
if short_call:
# Place orders for the covered call if delta is between 0.42 and 0.18 and if the strike price is greater than the latest upper boiler band
# Sell the 20 ~ 40 delta call
req = MarketOrderRequest(
symbol=short_call['symbol'],
qty=1,
side='sell',
type='market',
time_in_force='day'
)
trade_client.submit_order(req)
success_message = (f"Placing Coverd Call on {underlying_symbol} successfully:\n"
f"Sell {short_call['delta']} Delta Put: {short_call['symbol']} "
f"(Strike: {short_call['strike_price']}, Premium to Receive: {short_call['option_price']})")
return success_message, short_call
else:
return "Could not find suitable options which has delta between 20 and 40.", None
else:
return "No call options available for the underlying symbol.", NoneThe line of code below executes the covered call portion of the wheel strategy by calling the execute_covered_call function.
message, short_call = execute_covered_call(underlying_symbol, RISK_FREE_RATE, latest_upper_bollinger_band, short_put, max_strike, min_expiration, max_expiration)Step 5: Rinse or Roll the Put Option / Call Option
This step is optional, but traders may choose to implement it for added flexibility. Rolling can be applied at two points in the wheel strategy: after selling the cash-secured put or after selling the covered call.
By rolling, they can maintain the position while adjusting for market changes, potentially collecting additional premium. Traders may also rinse (close and re-enter) the put or call options after the covered call phase to restart the cycle if desired.
For example, rolling the put option involves:
- Buying back the current put.
- Selling a new put with a different strike price or expiration date.
This is useful if the stock price approaches the strike price, or volatility increases, making the existing position less favorable. If you want to avoid assignments, you can also use this technique.
The function roll_rinse_execution automates the process of closing an existing option position and optionally re-entering the market with a new one. It plays a dual role depending on whether the rolling parameter is set to True:
If rolling=True:
- The function closes the current option position (e.g., a cash-secured put or covered call) and opens a new one with a different strike price or expiration date.
- This is useful for managing risk, collecting additional premium, or avoiding assignment in unfavorable conditions.
If rolling=False:
- The function only closes the current position without re-entering the market.
- This may be done to exit the trade entirely, typically as part of a stop-loss or profit-taking strategy.
# Exit the market order
def roll_rinse_execution(option_data, rolling=True):
# if rolling the option, close the short put and re-enter the market with a new cash secured put or close the long call and re-enter the market with a new long call
if rolling:
# Deternine if the option is a call or put
option_type = option_data['type'].value
# If the option is a put, close the short put by buying it back
if option_type == 'put':
# Close the short put by buying it back
req = MarketOrderRequest(
symbol=option_data['symbol'],
qty=1,
side='buy',
type='market',
time_in_force='day'
)
# Submit the order to close the short put
trade_client.submit_order(req)
print(f"Closed short {option_type} option: {option_data['symbol']} bought")
# Re-enter the market with a new cash secured put
rolling_message, short = execute_cash_secured_put(underlying_symbol, RISK_FREE_RATE, buying_power_limit)
if short:
# You can add the `rolling_message` from the `execute_cash_secured_put` function below to check if the short put or call is not sccessfully placed
return f"Re-entering market with new cash secured put on {option_data['underlying_symbol']}", short
else:
return f"Failed to re-enter market with new cash secured put on {option_data['underlying_symbol']}", None
# If the option is a call, close the short call by buying it back
else:
# Close the short call by buying it back
req = MarketOrderRequest(
symbol=option_data['symbol'],
qty=1,
side='buy',
type='market',
time_in_force='day'
)
# Submit the order to close the covered call (short call)
trade_client.submit_order(req)
print(f"Closing short {option_type} option: {option_data['symbol']} sold")
# Re-enter the market with a new covered call
rolling_message, short = execute_covered_call(underlying_symbol, RISK_FREE_RATE, buying_power_limit)
if short:
return f"Re-entering market with new covered call on {option_data['underlying_symbol']}", short
else:
return f"Failed to re-enter market with new covered call on {option_data['underlying_symbol']}", None
else:
# If the option is a put, close the short put by buying it back
if option_type == 'put':
# Close the short put by buying it back
req = MarketOrderRequest(
symbol=option_data['symbol'],
qty=1,
side='buy',
type='market',
time_in_force='day'
)
trade_client.submit_order(req)
return f"Closed short {option_type} option: {option_data['symbol']} bought", None
# If the option is a call, close the short call by buying it back
else:
# Close the short call by buying it back
req = MarketOrderRequest(
symbol=option_data['symbol'],
qty=1,
side='buy',
type='market',
time_in_force='day'
)
# Submit the order to close the covered call (short call)
trade_client.submit_order(req)
return f"Closing short {option_type} option: {option_data['symbol']} sold", NoneThe function roll_rinse_option evaluates whether an option position needs adjustment and determines the appropriate action (hold, roll, or exit). It works in conjunction with roll_rinse_execution to decide when to act:
Option Evaluation:
- The function calculates the current delta and compares it to a threshold, such as 2x the initial delta, or evaluates whether the current option price has hit the target profit level (e.g., 50% of the premium received).
- These criteria help automate decision-making based on predefined risk and reward parameters.
Rolling or Exiting:
- If the threshold is breached (e.g., delta exceeds the target delta level of 2x the initial delta or the premium reaches the target), the function calls
roll_rinse_executionto either roll the option (ifrolling=True) or exit the trade entirely. - If the criteria are not met, it holds the position and waits for the next evaluation.
# calculate the current delta of the option (rolling or rinsing)
def roll_rinse_option(option_data, rolling=True):
# Get the latest quote for the option price
option_symbol = option_data["symbol"]
option_quote_request = OptionLatestQuoteRequest(symbol_or_symbols=option_symbol)
option_quote = option_historical_data_client.get_option_latest_quote(option_quote_request)[option_symbol]
# Extract option details
current_option_price = (option_quote.bid_price + option_quote.ask_price) / 2
strike_price = float(option_data["strike_price"])
expiry = pd.Timestamp(option_data["expiration_date"])
print(f"option_symbol is {option_symbol}")
print(f"current option_price is {current_option_price}")
print(f"current strike price is {strike_price}")
# Deternine if the option is a call or put
option_type = option_data['type'].value
# If the option is a put, calculate the delta for the put option
if option_type == 'put':
# Calculate delta for each option
current_delta = calculate_delta(
option_price=current_option_price,
strike_price=strike_price,
expiry=expiry,
underlying_price=underlying_price,
RISK_FREE_RATE=RISK_FREE_RATE,
option_type='put'
)
# If the option is a call, calculate the delta for the call option
else:
current_delta = calculate_delta(
option_price=current_option_price,
strike_price=strike_price,
expiry=expiry,
underlying_price=underlying_price,
RISK_FREE_RATE=RISK_FREE_RATE,
option_type='call'
)
# Set target profit levels in two ways: 1) 50% of the initial credit received, 2) 2x the initial delta of the short put
target_profit_price = option_data['initial_option_price'] * 0.5 # 50% of credit received
initial_delta = option_data['initial_delta'] * 2 # Set target delta level at 2x the initial delta of the short put
# roll or rinse the option if the absoluete value of the current delta is greater than or equal to the initial delta
if abs(current_delta) >= abs(initial_delta) or current_option_price <= target_profit_price:
# Roll or rinse the option
rinsing_message, short = roll_rinse_execution(option_data, rolling=rolling)
# you can add the `rinsing_message` from the `roll_rinse_execution` function below to check if the short put or call is not sccessfully placed
return f"Current delta {current_delta} exceeds twice the initial delta {initial_delta} or the option price is less than 50% of the initial credit received. Executing roll/rinse.", short
else:
return f"Current delta {current_delta} is less than twice the initial delta {initial_delta} and the option price is greater than 50% of the initial credit received. Holding the position.", NoneThe line of code below executes the rolling or rinsing part of the wheel strategy by calling the roll_rinse_option function. By default, it rolls the strategy, but you can set it to False to rinse the strategy instead.
message, short = roll_rinse_option(option_data=short_put, rolling=True)
message, shortTools and Resources
Accurate and timely data is the backbone of a successful wheel strategy. Real-time data providers, like Alpaca, ensure access to up-to-date stock prices, option chains, and technical indicators, minimizing errors and enhancing decision-making. After all, even the best strategy cannot bring potential profit automatically if you enter the wrong market at the wrong time.
That is why backtesting and paper trading are indispensable for mastering the wheel strategy. Backtesting with historical data enables traders to evaluate the strategy's performance across different market conditions, helping identify weaknesses and optimize parameters. By simulating scenarios where the stock moves up, down, or remains stagnant, traders can assess potential risks and rewards comprehensively.
Paper trading, on the other hand, provides a risk-free environment to practice and refine the strategy, ensuring that setups are thoroughly tested before committing real capital. Together, these tools build confidence and prepare traders to handle real-world challenges with precision.
Conclusion
This practical framework highlights how traders can execute the wheel strategy with Alpaca’s Trading API and paper trading environment.
Remember that the wheel strategy offers a structured and repeatable method for generating income through options trading. Its core strengths lie in its flexibility—allowing traders to potentially profit in various market conditions—and its risk management through cash-secured puts and covered calls. However, it is not without risks, such as assignment at unfavorable prices or exposure to sharp market downturns.
For traders, success with the wheel strategy depends on taking a disciplined approach, careful selection of underlyings, and proper use of technical analyses like ATR, RSI, and Bollinger Bands. Whether you’re a beginner exploring options or an experienced trader seeking a reliable strategy, the options wheel strategy could be one worth exploring.
Options trading is not suitable for all investors due to its inherent high risk, which can potentially result in significant losses. Please read Characteristics and Risks of Standardized Options before investing in options.
Past hypothetical backtest results do not guarantee future returns, and actual results may vary from the analysis.
The Paper Trading API is offered by AlpacaDB, Inc. and does not require real money or permit a user to transact in real securities in the market. Providing use of the Paper Trading API is not an offer or solicitation to buy or sell securities, securities derivative or futures products of any kind, or any type of trading or investment advice, recommendation or strategy, given or in any manner endorsed by AlpacaDB, Inc. or any AlpacaDB, Inc. affiliate and the information made available through the Paper Trading API is not an offer or solicitation of any kind in any jurisdiction where AlpacaDB, Inc. or any AlpacaDB, Inc. affiliate (collectively, “Alpaca”) is not authorized to do business.
Please note that this article is for general informational purposes only and is believed to be accurate as of the posting date but may be subject to change. The examples above are for illustrative purposes only.
All investments involve risk, and the past performance of a security, or financial product does not guarantee future results or returns. There is no guarantee that any investment strategy will achieve its objectives. Please note that diversification does not ensure a profit, or protect against loss. There is always the potential of losing money when you invest in securities, or other financial products. Investors should consider their investment objectives and risks carefully before investing.
Securities brokerage services are provided by Alpaca Securities LLC ("Alpaca Securities"), member FINRA/SIPC, a wholly-owned subsidiary of AlpacaDB, Inc. Technology and services are offered by AlpacaDB, Inc.
This is not an offer, solicitation of an offer, or advice to buy or sell securities or open a brokerage account in any jurisdiction where Alpaca Securities are not registered or licensed, as applicable.