Long straddles are a multi-leg options strategy designed for traders anticipating significant price volatility in an underlying asset without a clear directional bias. In this tutorial, we will explore the fundamentals of long straddles, providing real-world examples and discussing how market factors, including the Greeks, influence their performance. We will also explore the risks and nuances that every trader should understand before executing this strategy.

By breaking down the mechanics and construction of a long straddle, our guide aims to equip readers with the knowledge needed to harness volatility and optimize their trading approach effectively.  Then, we will highlight actionable steps you can take for algorithmic integration using Alpaca's Trading API or manual trading using Alpaca’s dashboard.

What Is A Long Straddle?

The long straddle is an advanced options trading strategy designed to seek potential gains from significant price movement in either direction, though outcomes depend on market conditions and execution. It involves buying a call option and a put option at the same strike price and expiration date, both of which are at-the-money (ATM). 

The put option provides potential gains if the underlying price drops while the call option provides potential gains if the underlying price rises. Because of this structure, the strategy does not require an accurate directional forecast but instead expects significant movement.

When to Use a Long Straddle

As mentioned, the long straddle may be utilized when traders expect strong price movements in the underlying asset in either direction. These market conditions include:

• Expectations of high implied volatility (IV): This strategy may be beneficial if a long straddle is entered when IV is relatively low and then increases afterward, as this typically raises the value of both options.
• Anticipation of a major price movement: This can occur due to upcoming earnings reports, economic or product announcements, FDA decisions, or geopolitical events.

Meanwhile, there are some situations where a long straddle might not be ideal.

• Low volatility environments: If price movement remains limited, time decay can erode the value of the options.
• Strong directional bias: A trader with a clear directional forecast may consider other strategies, such as buying a call or put.
• Significant time decay (Theta risk): As expiration approaches, both options may lose value if the asset price remains near the strike price.

Long Straddle Example (with Profit and Loss Diagram)

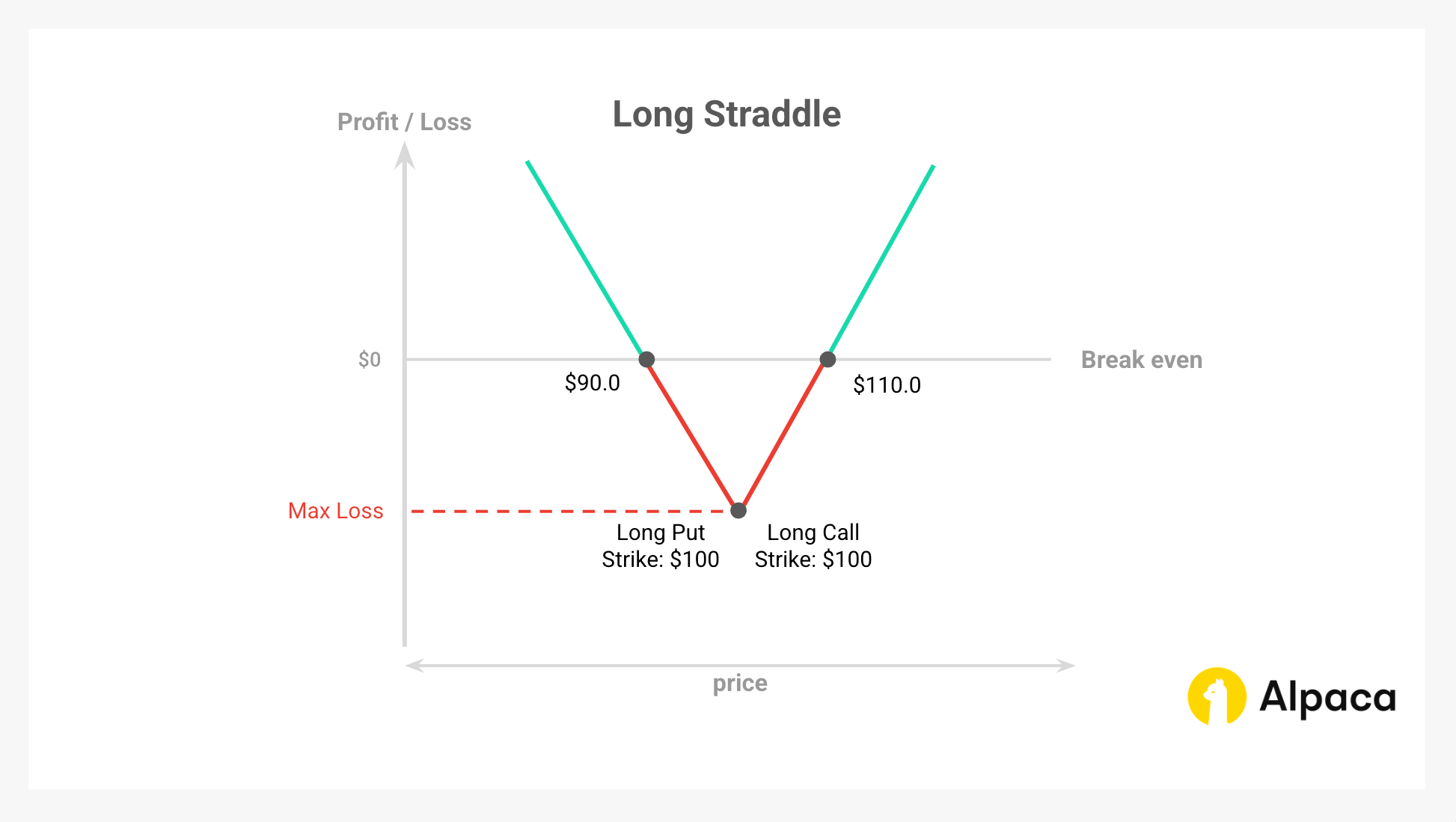
To understand how a long straddle performs under various market conditions, let's analyze its example using stock XYZ as the underlying asset. This will help illustrate the risk-reward profile of a long straddle, where the theoretical maximum loss is limited to the initial net debit of $10 per share, and the profit potential is theoretically unbounded if the price moves significantly in either direction.

Example Setup:

• Stock Price at Initiation: XYZ is trading at $100
• Strike Price: $100
• Initial Cost (Net Debit): -$1,000 (the total cost of buying the two options)
• Breakeven Points:
  • Upper breakeven: $100 + $10 = $110
  • Lower breakeven: $100 + $4 = $104

Trade Structure:

Potential Outcomes at Expiration:

Scenario 1: Stock remains at $100

• The call and put options expire worthless.
• The trader loses the full net debit of $5 per share ($1,000 total for two contracts).
• Net loss: -$1,000 (initial debit = theoretical maximum loss)

Scenario 2: Stock rises to $110

• The call option is in-the-money (ITM) with an intrinsic value of $10.
• The put option expires worthless.
• The trader breaks even at $110, covering the initial $10 premium paid.
• Breakeven: $11,000 (selling at market price) - $10,000 (exercising the long call) - $1,000 (initial debit) = $0

Scenario 3: Stock rises to $120

• The call option is ITM with an intrinsic value of $20.
• The put option expires worthless.
• The trader realizes a net profit of $10 per share ($1,000 total) after subtracting the initial $10 cost (- $1,000 total).
• Net profit: $2,000 (profit on the long call) - $1,000 (initial debit) = $1,000

Scenario 4: Stock falls to $80

• The put option is ITM with an intrinsic value of $20.
• The call option expires worthless.
• The trader realizes a net profit of $20 per share ($1,000 total) after subtracting the initial $10 cost (- $1,000 total).
• Net profit: $2,000 (profit on the long put) - $1,000 (initial debit) = $1,000

Understanding the Greeks and Implied Volatility in a Long Straddle

To optimize strategy execution when using a long straddle, it is essential to monitor volatility trends, price movements, and expiration timelines, as various option Greek factors can influence the outcome.

Delta (Directional Exposure)

• A long straddle starts as delta-neutral, meaning the net delta is close to zero.
• As the underlying price moves away from the strike price, one option gains value while the other loses value, causing delta to shift in the direction of the price movement.

Gamma (Rate of Change of Delta)

• A long straddle has high gamma, meaning delta changes rapidly as the stock price moves.
• The closer the option is to expiration, the more gamma increases, making the position more sensitive to small price changes.

Theta (Time Decay)

• Theta represents time decay, which negatively affects both options in a long straddle.
• If the stock price remains near the strike price, time decay erodes the value of both options at an accelerating rate as expiration approaches.

Vega (Volatility Impact)

• Vega measures sensitivity to implied volatility (IV). A long straddle benefits from increasing IV, as this raises the price of both the call and put options.
• If IV decreases after entering the trade, the option premiums may decline, leading to potential losses.

Implied Volatility

• Implied volatility, while not a Greek, is a critical factor in pricing options, reflecting the market's expectations for future price fluctuations.
• A long straddle is most effective when IV is relatively low at entry and expected to rise, as increasing IV boosts the premiums of both options.
• If IV is already high at the time of entering the trade, the risk of a volatility crash (IV declining after an event, such as earnings) increases, potentially leading to losses even if the stock moves significantly.
• Traders may want to analyze historical IV trends and upcoming catalysts that may impact volatility before entering a long straddle position.

Long Straddle vs Short Straddle

The long straddle and short straddle strategies are inverse to each other. Where the long straddle profits from significant price movement, the short straddle benefits from minimal price movement and stable volatility.

A trader typically chooses a long straddle for high volatility or a short straddle for stability and premium income. Due to the short straddle’s high risk, traders may hedge with iron condors or iron butterflies to limit losses.

Long Straddle vs Long Strangle

The long straddle and long strangle strategies are similar in that both aim to profit from significant price movements, but they differ in their cost structure and breakeven points, making them suitable for different volatility expectations.

Risk Management and Considerations of Long Straddles

Effective risk management is essential when trading long straddles to mitigate potential losses and optimize returns.

• Risk of Loss: The maximum risk is the total premium paid. If the underlying asset does not move enough, losses may occur due to time decay.
• Stop-Loss and Exit Strategies: Traders may set stop-loss levels to help limit potential losses. Exiting the trade before expiration can help capture profits if volatility increases.
• Position Sizing: Managing position size based on risk tolerance is important. Account for potential losses in risk management.
• Impact of Implied Volatility: High IV before entry may make options expensive, increasing risk. Low IV before entry may be more favorable.
• Early Exercise Risk: Since both options are long positions, early exercise is rare but possible.

Dividend Assignment Risk: Early assignment risk may increase on a stock’s ex-dividend date, especially for short call options, as holders may exercise to profit from the dividend-premium difference

Building a Long Straddle Strategy With Alpaca’s Trading API

This section provides a step-by-step guide to implementing a long straddle using Python and Alpaca’s Trading API in the Paper Trading environment. The strategy is a two-legged, neutral strategy that involves simultaneously buying both an ATM call and put options. This approach helps manage risk and optimize decision-making by leveraging key metrics and filters. If you’re not connected to Alpaca’s API or are unfamiliar with options trading, here are some useful resources to help you follow along:

• Sign up for an Alpaca Trading API account
• How to Connect to Alpaca's Trading API
• How to Start Paper Trading with Alpaca's Trading API
• How to Trade Options with Alpaca’s Trading API
• A Guide to Emotionless Options Trading

Important Notes:

• The code assumes a flat interest rate, excludes dividends, and is not optimized for 0DTE options. It does not consider market hours and serves as a starting point rather than a complete strategy.
• Expiration Day Order Rules:
  • Orders must be submitted before 3:15 p.m. ET for stocks/options and 3:30 p.m. ET for broad-based ETFs (e.g., SPY, QQQ).
  • Orders placed after these times will be rejected.
  • Expiring positions are auto-liquidated at 3:30 p.m. ET (stocks/options) and 3:45 p.m. ET (broad-based ETFs) for risk management.
• Multi-Leg (MLeg) Orders:
  • All legs of a strategy must be included in the same order for acceptance.
  • This is crucial for strategies with uncovered short options (e.g., short put calendar spreads, short call calendar spreads), which require Level 4 approval. See Alpaca's multi-leg order restrictions for details.
• American-Style Options Considerations:
  • American-style options may be assigned early, affecting trade outcomes. Profit/loss scenarios assume expiration without early exercise and do not factor in transaction fees (e.g., brokerage fees, commissions). Traders should also monitor ex-dividend dates for short calls to manage assignment risk.
• Example equity:
  • "AAPL" is used for demonstration purposes and should not be considered investment advice.

Setting Up the Environment and Trade Parameters

The first step involves configuring the environment for trading a long straddle and specifying your Alpaca Paper Trading API keys. This ensures your API connections and variable setup are secure and streamlined for data retrieval and trading operations. 

Note: While we are using Jupyter Notebook for this tutorial, you can use Google Collab or any other IDE as your code environment. You can also find all of the below code on Alpaca’s Github page.

# Install or upgrade the package `alpaca-py` and import it
!python3 -m pip install --upgrade alpaca-py

import pandas as pd
import numpy as np
from scipy.stats import norm
import alpaca
import time
from scipy.optimize import brentq
from datetime import datetime, timedelta
from zoneinfo import ZoneInfo
from alpaca.data.timeframe import TimeFrame, TimeFrameUnit
from dotenv import load_dotenv
import os

from alpaca.data.historical.option import OptionHistoricalDataClient
from alpaca.data.historical.stock import StockHistoricalDataClient, StockLatestTradeRequest
from alpaca.data.requests import StockBarsRequest, OptionLatestQuoteRequest, OptionChainRequest, OptionBarsRequest
from alpaca.trading.client import TradingClient
from alpaca.trading.requests import (
    MarketOrderRequest,
    GetOptionContractsRequest,
    MarketOrderRequest,
    OptionLegRequest,
    ClosePositionRequest,
)
from alpaca.trading.enums import (
    AssetStatus,
    ExerciseStyle,
    OrderSide,
    OrderClass,
    OrderStatus,
    OrderType,
    TimeInForce,
    QueryOrderStatus,
    ContractType,
)

The script initializes Alpaca clients for trading stocks and options, as well as for handling data requests.

# API credentials for Alpaca API
API_KEY = "YOUR_ALPACA_API_KEY_FOR_PAPER_TRADING"
API_SECRET = 'YOUR_ALPACA_API_SECRET_KEY_FOR_PAPER_TRADING'
BASE_URL = None
## We use a paper environment for this example (Please do not modify this. This example is for paper trading only)
PAPER = True

# Initialize Alpaca clients
trade_client = TradingClient(api_key=API_KEY, secret_key=API_SECRET, paper=PAPER, url_override=BASE_URL)
option_historical_data_client = OptionHistoricalDataClient(api_key=API_KEY, secret_key=API_SECRET, url_override=BASE_URL)
stock_data_client = StockHistoricalDataClient(api_key=API_KEY, secret_key=API_SECRET)

# Below are the variables for development this documents
# Please do not change these variables
trade_api_url = None
trade_api_wss = None
data_api_url = None
option_stream_data_wss = None

Calculations for Implied Volatility and Option Greeks with Black-Scholes model

The calculate_implied_volatility function estimates implied volatility (IV) using the Black-Scholes model. The function defines a reasonable range for sigma (1e-6 to 5.0) to avoid extreme values. For deep out-of-the-money (OTM) options where the price is close to intrinsic value, the function directly sets IV to 0.0 to prevent calculation errors. A numerical root-finding method is used to solve for IV, ensuring accuracy even in edge cases.

# Calculate implied volatility
def calculate_implied_volatility(option_price, S, K, T, r, option_type):
    
    # Define a reasonable range for sigma
    sigma_lower = 1e-6
    sigma_upper = 5.0  # Adjust upper limit if necessary

    # Check if the option is out-of-the-money and price is close to zero
    intrinsic_value = max(0, (S - K) if option_type == 'call' else (K - S))
    if option_price <= intrinsic_value + 1e-6:
        
        print('Option price is close to intrinsic value; implied volatility is near zero.')
        return 0.0
    
    # Define the function to find the root
    def option_price_diff(sigma):
        d1 = (np.log(S / K) + (r + 0.5 * sigma ** 2) * T) / (sigma * np.sqrt(T))
        d2 = d1 - sigma * np.sqrt(T)
        if option_type == 'call':
            price = S * norm.cdf(d1) - K * np.exp(-r * T) * norm.cdf(d2)
        elif option_type == 'put':
            price = K * np.exp(-r * T) * norm.cdf(-d2) - S * norm.cdf(-d1)
        return price - option_price

    try:
        return brentq(option_price_diff, sigma_lower, sigma_upper)
    except ValueError as e:
        print(f"Failed to find implied volatility: {e}")
        return None

The calculate_greeks function estimates all option Greeks: delta, gamma, theta, and vega based on the implied volatility calculated through calculate_implied_volatility. In this demonstration, we mainly use delta and theta as well as implied volatility.

def calculate_greeks(option_price, strike_price, expiration, underlying_price, risk_free_rate, option_type):
    T = (expiration - pd.Timestamp.now()).days / 365 # It is unconventional, but some use 225 days (# of annual trading days) in replace of 365 days
    T = max(T, 1e-6)  # Set minimum T to avoid zero
    
    if T == 1e-6:
        print('Option has expired or is expiring now; setting Greeks based on intrinsic value.')
        if option_type == 'put':
            delta = -1.0 if underlying_price < strike_price else 0.0
        else:
            delta = 1.0 if underlying_price > strike_price else 0.0
        gamma = 0.0
        theta = 0.0
        vega = 0.0
        return delta, gamma, theta, vega
    
    # Calculate IV
    IV = calculate_implied_volatility(option_price, underlying_price, strike_price, T, risk_free_rate, option_type)

    if IV is None or IV == 0.0:
        print('Implied volatility could not be determined, skipping Greek calculations.')
        return None
    
    d1 = (np.log(underlying_price / strike_price) + (risk_free_rate + 0.5 * IV ** 2) * T) / (IV * np.sqrt(T))
    d2 = d1 - IV * np.sqrt(T) # d2 for Theta calculation
    # Calculate Delta
    delta = norm.cdf(d1) if option_type == 'call' else -norm.cdf(-d1)
    # Calculate Gamma
    gamma = norm.pdf(d1) / (underlying_price * IV * np.sqrt(T))
    # Calculate Vega
    vega = underlying_price * np.sqrt(T) * norm.pdf(d1) / 100
    # Calculate Theta
    if option_type == 'call':
        theta = (
            - (underlying_price * norm.pdf(d1) * IV) / (2 * np.sqrt(T))
            - (risk_free_rate * strike_price * np.exp(-risk_free_rate * T) * norm.cdf(d2))
        )
    else:
        theta = (
            - (underlying_price * norm.pdf(d1) * IV) / (2 * np.sqrt(T))
            + (risk_free_rate * strike_price * np.exp(-risk_free_rate * T) * norm.cdf(-d2))
        )
    # Convert annualized theta to daily theta
    theta /= 365
    
    return delta, gamma, theta, vega

Pick Your Strategy Inputs: Right Strike Price and Expiration

Underlying Price and Strike Range

The script retrieves the current AAPL price via Alpaca’s market data, then calculates the minimum and maximum strike prices by multiplying that price by (1 - 0.05) and (1 + 0.05), respectively. This ensures that the strike range covers ±5% around the market price.

Expiration Dates

The code sets a global minimum (today + 14 days) and maximum (today + 60 days) for potential expirations. However, we further refine it to a common range of 14 to 42 days. This means the final options that are picked for the long call and long put must fall within that 14–42 day window, which is a common range for short to medium-term directional strategies or event-driven trades.

Additionally, the script incorporates a risk-free rate of 1% (0.01) in internal calculations, enhancing the accuracy of implied volatility and Greek metrics, particularly vega and gamma. This helps fine-tune pricing models and ensures a more precise evaluation of the straddle’s risk and reward dynamics.

Pick Your Strategy Inputs: Risk Management and Position Sizing

Liquidity and Open Interest Threshold

To avoid thinly traded contracts, we’ve defined an Open Interest (OI) threshold of 100. That means that when scanning the option chain, the code would only consider options that meet or exceed this OI figure, helping ensure that spreads remain tighter and execution is smoother.

Option Greeks and IV Ranges

In the criteria dictionary, each leg of the straddle (long put and long call) also has implied volatility (IV) ranges (0.30–0.65) and delta ranges (e.g., -0.50 to -0.10 for the put, 0.10 to 0.50 for the call). This reflects the desire to target options that are:

1. Reasonably priced from a volatility perspective (not excessively expensive).
2. Not too deep ITM or OTM (so the long straddle remains balanced).

Target Profit

A target profit percentage of 40% means we’re looking to close the entire straddle (or part of it) once the value of the combined position is up 40% from the initial debit. This helps lock in gains if the underlying moves significantly in either direction or if implied volatility spikes in our favor.

Buying Power Allocation

The code checks the account buying power and designates that only 5% (BUY_POWER_LIMIT = 0.05) of the available funds should be used for the trade. This is a prudent measure to avoid overexposure, especially given that a long straddle can risk the entire premium if the market doesn’t move as expected.

Evaluating the Cost

Once the suitable options (meeting the strike, expiration, IV, delta, and OI criteria) are identified, the code calculates the total cost of buying one call and one put. Multiplying by 100 (since each contract typically represents 100 shares) gives us the final cost per straddle. We then compare that cost against our buying_power_limit to ensure we stay within the 5% capital allocation rule.

Monitoring and Potential Adjustments

Although the code doesn’t explicitly detail how to monitor or close the trade, the TARGET_PROFIT_PERCENTAGE = 0.4 provides a clear exit guideline. Traders can set up alerts or automate an exit when the straddle’s value appreciates by 40%. If the underlying stagnates or implied volatility drops, some traders may also establish a theoretical maximum loss threshold (e.g., 50% of the premium paid) to limit drawdowns.

Liquidity Considerations and Stop-Loss Limits

Because we set an open interest threshold (OI_THRESHOLD = 100), we’re already filtering out illiquid strikes. Still, be mindful that in a fast-moving market, option prices can gap, and a typical stop-loss order may trigger at less favorable prices. A common practice is often to monitor the position actively or use limit orders to exit, ensuring we don’t face excessive slippage.

# Select the underlying stock (Apple Inc.)
underlying_symbol = 'AAPL'

# Set the timezone
timezone = ZoneInfo('America/New_York')

# Get current date in US/Eastern timezone
today = datetime.now(timezone).date()

# Define a 5% range around the underlying price 
STRIKE_RANGE = 0.05

# Buying power percentage to use for the trade
BUY_POWER_LIMIT = 0.05

# Risk free rate for the options greeks and IV calculations
risk_free_rate = 0.01

# Check account buying power
buying_power = float(trade_client.get_account().buying_power)

# Set the open interest volume threshold
OI_THRESHOLD = 100

# Calculate the limit amount of buying power to use for the trade
buying_power_limit = buying_power * BUY_POWER_LIMIT

# Set the expiration date range for the options
min_expiration = today + timedelta(days=14)
max_expiration = today + timedelta(days=60)

# Get the latest price of the underlying stock
def get_underlying_price(symbol):
    # Get the latest trade for the underlying stock
    underlying_trade_request = StockLatestTradeRequest(symbol_or_symbols=symbol)
    underlying_trade_response = stock_data_client.get_stock_latest_trade(underlying_trade_request)
    return underlying_trade_response[symbol].price

# Get the latest price of the underlying stock
underlying_price = get_underlying_price(underlying_symbol)

# Set the minimum and maximum strike prices based on the underlying price
min_strike = str(underlying_price * (1 - STRIKE_RANGE))
max_strike = str(underlying_price * (1 + STRIKE_RANGE))

# Define a common expiration range for all legs between 14 days and 42 days
COMMON_EXPIRATION_RANGE = (14, 42)

# Each key corresponds to a leg and maps to a tuple of: (expiration range, IV range, delta range, theta range)
criteria = {
    'long_put':  (COMMON_EXPIRATION_RANGE, (0.30, 0.60), (-0.50, -0.10), (-0.1, -0.005)),
    'long_call': (COMMON_EXPIRATION_RANGE, (0.30, 0.60), (0.10, 0.50), (-0.1, -0.005))
}

# Set target profit levels
TARGET_PROFIT_PERCENTAGE = 0.4

# Display the values
print(f"Underlying Symbol: {underlying_symbol}")
print(f"{underlying_symbol} price: {underlying_price}")
print(f"Strike Range: {STRIKE_RANGE}")
print(f"Buying Power Limit Percentage: {BUY_POWER_LIMIT}")
print(f"Risk Free Rate: {risk_free_rate}")
print(f"Account Buying Power: {buying_power}")
print(f"Buying Power Limit: {buying_power_limit}")
print(f"Open Interest Threshold: {OI_THRESHOLD}")
print(f"Minimum Expiration Date: {min_expiration}")
print(f"Maximum Expiration Date: {max_expiration}")
print(f"Minimum Strike Price: {min_strike}")
print(f"Maximum Strike Price: {max_strike}")

Factors To Include In The Strategy

When implementing a long straddle, it's essential to identify market conditions that support the strategy. Using a combination of price trends, volatility measures, and technical indicators, traders would be able to optimize entry points and improve trade efficiency. The following factors may help the long straddle setups based on underlying asset price movement and volatility events.

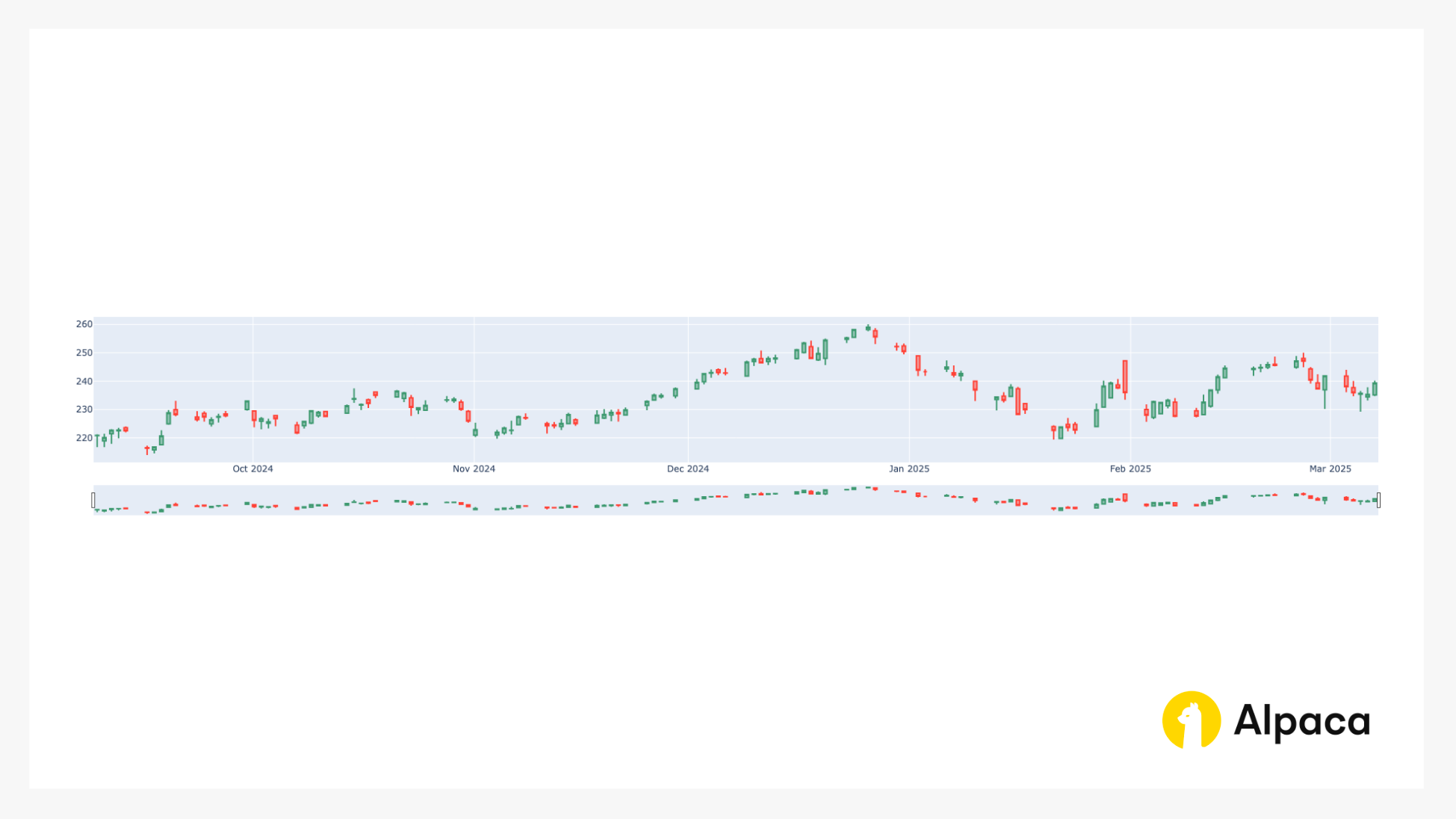
Stock Price Trends (Bar Chart Analysis)

Monitoring historical price movements helps traders assess the broader trend of the underlying asset. A candlestick chart provides insights into recent price action, as well as support and resistance levels, which can help determine whether the market is range-bound or trending. A long straddle strategy works in elevated-volatility environments where volatility is expected to decrease, keeping the underlying asset stable within a defined range.

# Get the historical data for the underlying stock by symbol and timeframe
# ref. https://alpaca.markets/sdks/python/api_reference/data/option/historical.html
def get_stock_data(underlying_symbol, days=90):
    today = datetime.now(timezone).date()
    req = StockBarsRequest(
        symbol_or_symbols=[underlying_symbol],
        timeframe=TimeFrame(amount=1, unit=TimeFrameUnit.Day),     # specify timeframe
        start=today - timedelta(days=days),                          # specify start datetime, default=the beginning of the current day.
    )
    return stock_data_client.get_stock_bars(req).df

# List of stock agg objects while dropping the symbol column
priceData = get_stock_data(underlying_symbol, days=365).reset_index(level='symbol', drop=True)

import plotly.graph_objects as go

# Bar chart for the stock price
fig = go.Figure(data=[go.Candlestick(x=priceData.index,
                open=priceData['open'],
                high=priceData['high'],
                low=priceData['low'],
                close=priceData['close'])])

fig.show()

This code returns the bar chart like in the image below.

Relative Volatility Index (RVI)

The Relative Volatility Index (RVI) measures the strength of price momentum relative to volatility. It helps confirm whether the market is experiencing increased price fluctuations or stabilizing.

If the RVI is between 40 and 60, it suggests a moderately neutral volatility movement, which may be favorable as an entry point for a long straddle strategy. Conversely, a low or declining RVI may indicate a stable market environment, making it a less favorable setup at the time of entry. However, since volatility contraction possibly benefits the strategy by accelerating premium decay in the sold options, it is important to actively monitor the RVI.

def calculate_rvi(df, period):
    # Calculate daily price changes 
    df['price_change'] = df['close'].diff()

    # Separate up and down price changes
    df['up_change'] = df['price_change'].where(df['price_change'] > 0, 0)
    df['down_change'] = -df['price_change'].where(df['price_change'] < 0, 0)

    # Calculate std of up and down changes over the rolling period
    df['avg_up_std'] = df['up_change'].rolling(window=period).std()
    df['avg_down_std'] = df['down_change'].rolling(window=period).std()

    # Calculate RVI
    df['rvi'] = 100 - (100 / (1 + (df['avg_up_std'] / df['avg_down_std'])))

    # Smooth the RVI with a 4 periods moving average
    df['rvi_smoothed'] = df['rvi'].rolling(window=4).mean()

    return df['rvi_smoothed']

# smoothed RVI
calculate_rvi(priceData, period=21).iloc[30:]

Bollinger Bands for Volatility Assessment

Bollinger Bands provide a dynamic range around the asset's price, helping to gauge market volatility. When the underlying stock price is near the upper Bollinger Band, it may indicate overbought conditions, while a price near the lower band suggests oversold levels. 

Long straddles potentially benefit from heightened volatility when its expiry is close, where both the call and put options experience increased extrinsic value due to higher implied volatility, leading to potential gains regardless of the direction of the price movement. If the asset is trading closer to the upper or lower Bollinger Band, it signifies a profit potential.

# setup bollinger band calculations
def check_bb(df, period=14, multiplier=2):
    bollinger_bands = []
    # Calculate the Simple Moving Average (SMA)
    df['SMA'] = df['close'].rolling(window=period).mean()
    # Calculate the rolling standard deviation
    df['StdDev'] = df['close'].rolling(window=period).std()
    # Calculate the Upper Bollinger Band (two standard deviation)
    df['Upper Band'] = df['SMA'] + (multiplier * df['StdDev'])
    # Calculate the Lower Bollinger Band (two standard deviation)
    df['Lower Band'] = df['SMA'] - (multiplier * df['StdDev'])
    # Get the most recent Upper Band value
    upper_bollinger_band = df['Upper Band'].iloc[-1]
    lower_bollinger_band = df['Lower Band'].iloc[-1]
    
    bollinger_bands = [upper_bollinger_band, lower_bollinger_band]
    return bollinger_bands

bollinger_bands = check_bb(priceData, 14, 2)

# The current market price is not too close to the two-standard deviation level yet but is relatively closer to the higher Bollinger Band.
print(f"Latest Upper Bollinger Band is: {bollinger_bands[0]}. Latest Lower Bollinger Band is {bollinger_bands[1]}; while underlying stock '{underlying_symbol}' price is {underlying_price}.")

Set up for A Long Straddle (Find both put and call options)

The get_options function retrieves active option contracts for a specified underlying symbol within a given strike price and expiration date range. Reminder to specify option_type as either ContractType.CALL or ContractType.PUT to filter for the desired option type.

# option_type: ContractType.CALL or ContractType.PUT.
def get_options(underlying_symbol, min_strike, max_strike, min_expiration, max_expiration, option_type):
    req = GetOptionContractsRequest(
        underlying_symbols=[underlying_symbol],
        status=AssetStatus.ACTIVE,
        type=option_type,
        strike_price_gte=min_strike,
        strike_price_lte=max_strike,
        expiration_date_gte=min_expiration,
        expiration_date_lte=max_expiration,        
    )
    return trade_client.get_option_contracts(req).option_contracts

The helper function validate_sufficient_OI verifies that an option's data includes the necessary fields and that its open interest exceeds a specified threshold. It is used at the start of the workflow to ensure that only eligible options are processed further.

def validate_sufficient_OI(option_data, OI_THRESHOLD):
    '''Ensure that the option has the required fields and sufficient open interest.'''
    if option_data.open_interest is None or option_data.open_interest_date is None:
        return False
    if float(option_data.open_interest) <= OI_THRESHOLD:
        return False
    return True

The function build_option_dict constructs an option dictionary from option data and its calculated metrics. It is used within both group_and_select_common_expiration to store details for a long straddle.

def build_option_dict(option_data, underlying_price, risk_free_rate):
    '''
    Helper to build an option dictionary from option_data and calculated metrics.
    '''
    # Retrieve the latest quote
    option_quote_req = OptionLatestQuoteRequest(symbol_or_symbols=option_data.symbol)
    option_quote = option_historical_data_client.get_option_latest_quote(option_quote_req)[option_data.symbol]
    option_price = (option_quote.bid_price + option_quote.ask_price) / 2

    strike_price = float(option_data.strike_price)
    expiration = pd.Timestamp(option_data.expiration_date)
    remaining_days = (expiration - pd.Timestamp.now()).days

    iv = calculate_implied_volatility(
        option_price=option_price,
        S=underlying_price,
        K=strike_price,
        T=max(remaining_days / 365, 1e-6),
        r=risk_free_rate,
        option_type=option_data.type.value
    )
    delta, _, theta, _ = calculate_greeks(
        option_price=option_price,
        strike_price=strike_price,
        expiration=expiration,
        underlying_price=underlying_price,
        risk_free_rate=risk_free_rate,
        option_type=option_data.type.value
    )

    # Build a candidate dictionary that can be augmented or returned
    candidate = {
        'id': option_data.id,
        'name': option_data.name,
        'symbol': option_data.symbol,
        'strike_price': option_data.strike_price,
        'root_symbol': option_data.root_symbol,
        'underlying_symbol': option_data.underlying_symbol,
        'underlying_asset_id': option_data.underlying_asset_id,
        'close_price': option_data.close_price,
        'close_price_date': option_data.close_price_date,
        'expiration': expiration,
        'remaining_days': remaining_days,
        'open_interest': option_data.open_interest,
        'open_interest_date': option_data.open_interest_date,
        'size': option_data.size,
        'status': option_data.status,
        'style': option_data.style,
        'tradable': option_data.tradable,
        'type': option_data.type,
        'initial_IV': iv,
        'initial_delta': delta,
        'initial_theta': theta,
        'initial_option_price': option_price,

    }
    return candidate

The function check_candidate_option_conditions checks if a candidate option meets the filtering criteria provided as a tuple (expiration range, IV range, delta range, theta range). It is used within the main workflow to determine whether a candidate qualifies for a specific leg of the long straddle.

def check_candidate_option_conditions(candidate, criteria, label):
    '''
    Check whether a candidate option meets the filtering criteria.
    The criteria is a tuple of (expiration_range, iv_range, delta_range, theta_range).
    '''
    expiration_range, iv_range, delta_range, theta_range = criteria

    if not (expiration_range[0] <= candidate['remaining_days'] <= expiration_range[1]):
        print(f"{candidate['symbol']} fails expiration condition for {label}.")
        return False
    if not (iv_range[0] <= candidate['initial_IV'] <= iv_range[1]):
        print(f"{candidate['symbol']} fails IV condition for {label}.")
        return False
    if not (delta_range[0] <= candidate['initial_delta'] <= delta_range[1]):
        print(f"{candidate['symbol']} fails delta condition for {label}.")
        return False
    if not (theta_range[0] <= candidate['initial_theta'] <= theta_range[1]):
        print(f"{candidate['symbol']} fails theta condition for {label}.")
        return False

    return True

The group_and_select_common_expiration function processes put and call options, grouping them by expiration date and selecting a common expiration that contains valid candidates for both option types. 

It first filters options based on open interest and builds candidate dictionaries. It then determines common expiration dates and selects the one with the most candidates. This function ensures that the long straddle has both legs (put and call) with the same expiration.

def group_and_select_common_expiration(put_options, call_options, underlying_price, risk_free_rate, criteria, OI_THRESHOLD):
    """
    Processes put and call options, groups valid candidates by expiration, and selects a common expiration.
    
    Returns:
      selected_expiration: The chosen expiration date.
      put_candidates: List of long put candidates for that expiration.
      call_candidates: List of long call candidates for that expiration.
    """
    put_candidates_by_exp = {}
    call_candidates_by_exp = {}

    # Process put options
    # Iterate through each put option, validate its open interest, build its candidate dictionary, and group the candidate by its expiration date. 
    for option_data in put_options:
        if not validate_sufficient_OI(option_data, OI_THRESHOLD):
            continue
        candidate = build_option_dict(option_data, underlying_price, risk_free_rate)
        expiration = candidate['expiration']
        put_candidates_by_exp.setdefault(expiration, [])
        # Check if the candidate meets the long put criteria and add it to the appropriate expiration group.
        if check_candidate_option_conditions(candidate, criteria['long_put'], 'long_put'):
            put_candidates_by_exp[expiration].append(candidate)
            print(f"Added {candidate['symbol']} as a long put candidate for expiration {expiration}.")

    # Process call options
    # Iterate through each call option, validate its open interest, build its candidate dictionary, and group the candidate by its expiration date. 
    for option_data in call_options:
        if not validate_sufficient_OI(option_data, OI_THRESHOLD):
            continue
        candidate = build_option_dict(option_data, underlying_price, risk_free_rate)
        expiration = candidate['expiration']
        call_candidates_by_exp.setdefault(expiration, [])
        # Check if the candidate meets the long call criteria and add it to the appropriate expiration group.
        if check_candidate_option_conditions(candidate, criteria['long_call'], 'long_call'):
            call_candidates_by_exp[expiration].append(candidate)
            print(f"Added {candidate['symbol']} as a long call candidate for expiration {expiration}.")

    # Find common expiration dates
    common_expirations = set(put_candidates_by_exp.keys()).intersection(set(call_candidates_by_exp.keys()))
    if not common_expirations:
        raise Exception('No common expiration found across put and call candidates.')

    # Choose the expiration with the most candidates
    selected_expiration = max(common_expirations, key=lambda exp: len(put_candidates_by_exp[exp]) + len(call_candidates_by_exp[exp]))
    print(f"Selected common expiration: {selected_expiration}")
    
    return put_candidates_by_exp[selected_expiration], call_candidates_by_exp[selected_expiration]

The select_common_strike_candidate function identifies a common strike price among the filtered put and call candidates within the selected expiration date. 

It chooses the strike price closest to the underlying asset's price, ensuring a balanced long straddle structure. It then retrieves the corresponding put and call options with the chosen strike price, forming the core components of the strategy.

def select_common_strike_candidate(put_candidates, call_candidates, underlying_price):
    """
    Finds common strike prices between put and call candidates, selects the one closest to the underlying price,
    and returns one candidate from each side with that strike.
    
    Returns:
      selected_strike: The chosen strike price.
      chosen_put: A long put candidate with the selected strike.
      chosen_call: A long call candidate with the selected strike.
    """
    put_strikes = {float(cand['strike_price']) for cand in put_candidates}
    call_strikes = {float(cand['strike_price']) for cand in call_candidates}
    common_strikes = put_strikes.intersection(call_strikes)
    if not common_strikes:
        raise Exception("No common strike price found across put and call candidates for the selected expiration.")
    
    selected_strike = min(common_strikes, key=lambda strike: abs(strike - underlying_price))
    print(f"Selected common strike price: {selected_strike}")
    
    chosen_put = next((cand for cand in put_candidates if float(cand['strike_price']) == selected_strike), None)
    chosen_call = next((cand for cand in call_candidates if float(cand['strike_price']) == selected_strike), None)
    
    if not chosen_put or not chosen_call:
        raise Exception("Could not find valid candidate(s) with the selected strike price.")
    
    return chosen_put, chosen_call

The check_buying_power function evaluates whether the total cost of the long straddle (sum of the initial option premiums multiplied by contract size) fits within the buying power limit. 

If the calculated risk exceeds the available capital, an exception is raised, preventing further execution in the main function called find_options_for_long_straddle. This function ensures that the trade remains within the trader's financial constraints.

def check_buying_power(put_option, call_option, buying_power_limit):
    """
    Calculates the total premium paid (risk) for the long straddle and checks it against the buying power limit.
    If the buying power requirement is not met, the exception is thrown and the rest of the code is never executed.
    """
    option_size = float(put_option['size'])
    risk = (put_option['initial_option_price'] + call_option['initial_option_price']) * option_size
    print(f"Calculated long straddle risk: {risk}.")
    
    if risk >= buying_power_limit:
        raise Exception('Buying power limit exceeded for the long straddle risk.')

The find_options_for_long_straddle function orchestrates the selection process for constructing a long straddle. It first identifies valid options with a common expiration, then selects the best matching strike price for both legs. Finally, it verifies that the trade meets the buying power requirement before returning the chosen long put and long call options. This function streamlines the entire workflow of structuring a long straddle trade.

def find_options_for_long_straddle(call_options, put_options, underlying_price, risk_free_rate, buying_power_limit, criteria, OI_THRESHOLD):
    """
    Orchestrates the workflow to build a long straddle with a common expiration and common strike after checking the filtering criteria.
    
    Returns a list of legs in the order: [long_put, long_call]
    """
    # Group candidates by expiration and select the best common expiration
    put_candidates, call_candidates = group_and_select_common_expiration(
            put_options, 
            call_options, 
            underlying_price, 
            risk_free_rate, 
            criteria, 
            OI_THRESHOLD
    )
    
    # Within the selected expiration, choose the common strike and corresponding candidates
    chosen_long_put, chosen_long_call = select_common_strike_candidate(
        put_candidates, 
        call_candidates, 
        underlying_price
    )
    
    # Check buying power requirements
    check_buying_power(chosen_long_put, chosen_long_call, buying_power_limit)
    
    # Return the final long straddle legs
    long_straddle = [chosen_long_put, chosen_long_call]
    print('\nReturning long straddle legs:')

    for leg in long_straddle:
        print(f"{leg['symbol']} at strike {leg['strike_price']}")
    
    return long_straddle

Execute A Long Straddle Strategy

We now can run the find_options_for_long_straddle function to find a reasonable set of options for a long straddle.

call_options = get_options(underlying_symbol, min_strike, max_strike, min_expiration, max_expiration, ContractType.CALL)
put_options = get_options(underlying_symbol, min_strike, max_strike, min_expiration, max_expiration, ContractType.PUT)

long_straddle_order_legs = find_options_for_long_straddle(call_options, put_options, underlying_price, risk_free_rate, buying_power_limit, criteria, OI_THRESHOLD)

After running the code, we would see output similar to what is shown below, though it may vary depending on the specific conditions and stocks used.

AAPL250328C00235000 fails delta condition for long_call.
AAPL250328C00240000 fails delta condition for long_call.
Added AAPL250328C00245000 as a long call candidate for expiration 2025-03-28 00:00:00.
Added AAPL250328C00250000 as a long call candidate for expiration 2025-03-28 00:00:00.
Added AAPL250328C00255000 as a long call candidate for expiration 2025-03-28 00:00:00.
Insufficient open interest for put option AAPL250404C00235000 (threshold: 100). Skipping candidate.
AAPL250404C00240000 fails delta condition for long_call.
Added AAPL250404C00245000 as a long call candidate for expiration 2025-04-04 00:00:00.
Added AAPL250404C00250000 as a long call candidate for expiration 2025-04-04 00:00:00.
Added AAPL250404C00255000 as a long call candidate for expiration 2025-04-04 00:00:00.
AAPL250417C00235000 fails expiration condition for long_call.
AAPL250417C00240000 fails expiration condition for long_call.
AAPL250417C00245000 fails expiration condition for long_call.
AAPL250417C00250000 fails expiration condition for long_call.
AAPL250417C00255000 fails expiration condition for long_call.
Selected common expiration: 2025-03-21 00:00:00
Selected common strike price: 245.0
Calculated long straddle risk: 1285.5.

Returning long straddle legs:
AAPL250321P00245000 at strike 245.0
AAPL250321C00245000 at strike 245.0

The script below builds the list of options for the long straddle and places an order.

## Place orders for the long straddle spread if all options are found
if long_straddle_order_legs:
    # Create a list for the order request
    order_legs = []
    ## Append long put
    order_legs.append(OptionLegRequest(
        symbol=long_straddle_order_legs[0]["symbol"],
        side=OrderSide.BUY,
        ratio_qty=1
    ))
    ## Append long call
    order_legs.append(OptionLegRequest(
        symbol=long_straddle_order_legs[1]["symbol"],
        side=OrderSide.BUY,
        ratio_qty=1
    ))

    # Place the order for both legs simultaneously
    req = MarketOrderRequest(
        qty=1,
        order_class=OrderClass.MLEG,
        time_in_force=TimeInForce.DAY,
        legs=order_legs
    )
    res = trade_client.submit_order(req)
    print("Long Straddle order placed successfully.")

Before the order is filled, traders may choose to cancel it. Please note that individual legs cannot be canceled or replaced. You must cancel the entire order. If you are not familiar with the level 3 option trading with multi-legs, please check out an example code for multi-leg option trading on Alpaca’s Github page!

# Query by the order's id
q1 = trade_client.get_order_by_client_id(res.client_order_id)

# Replace overall order
if q1.status != OrderStatus.FILLED:
    # Cancel the whole order
    trade_client.cancel_order_by_id(res.id)
    print(f"Canceled order: {res}")

else:
    print("Order is already filled.")

The Importance of Backtesting A Long Straddle Strategy

Backtesting your options strategy is a critical step in developing a robust long straddle strategy, especially when implementing it in an algorithmic trading system. Given that the long straddle relies on volatility shifts (vega), and limited directional exposure (gamma), backtesting allows traders and quants to validate strategy performance before risking capital.

With Alpaca’s Trading API, you can not only backtest using an underlying asset’s historical data but also extract historical option data. The script below retrieves historical option data. However, accessing the latest OPRA data may require the Algo Trader Plus subscription. Meanwhile, the free 'Basic' account typically provides the necessary historical data.

# Initialize the Option Historical Data Client
option_historical_data_client = OptionHistoricalDataClient(
    api_key=API_KEY, 
    secret_key=API_SECRET, 
    url_override=BASE_URL
)

# Define the request parameters
req = OptionBarsRequest(
    #  iron_condor_order_legs[1]["symbol"] = the short put option
    symbol_or_symbols=iron_condor_order_legs[1]["symbol"],
    timeframe=TimeFrame.Day,  # Choose timeframe (Minute, Hour, Day, etc.)
    start="2025-01-01",  # Start date
    end="2025-03-14"  # End date
)

option_historical_data_client.get_option_bars(req)

Trading A Long Straddle on Alpaca’s Dashboard

You can also execute a long straddle using Alpaca’s dashboard manually. Please note we are using AAPL as an example and it should not be considered investment advice.

1. Log in to your account

Sign in to your account and navigate to the “Home” page.

2. Find your desired trade

On your dashboard in the top left, you can select between using your paper trading or live accounts. It’s important that you select the appropriate trading account before implementing an options strategy. If you want to practice without the risk of real capital, you can use your paper trading accounts. If you are looking to implement strategies, you can use your live account.

Once you’ve selected the desired account within your dashboard, you can monitor your portfolio, access market data, execute trades, and review your trading history. In order to create your first options trade, use the search bar to find and select the applicable option ticker symbol.

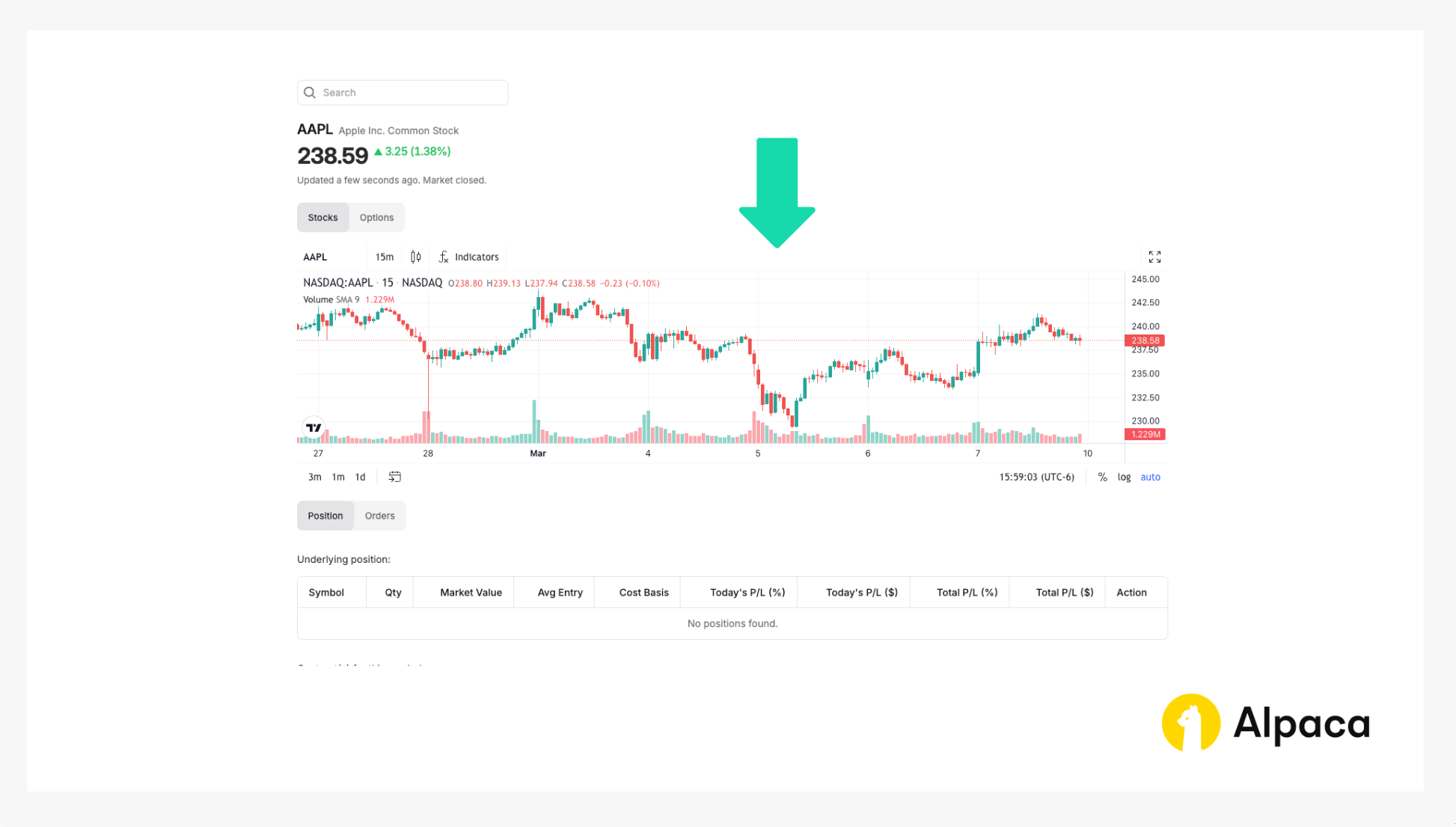
3. Check underlying security’s bar chart

If you search the desired underlying asset, a page shows the asset’s bar chart. You can use this bar chart for a simple analysis.

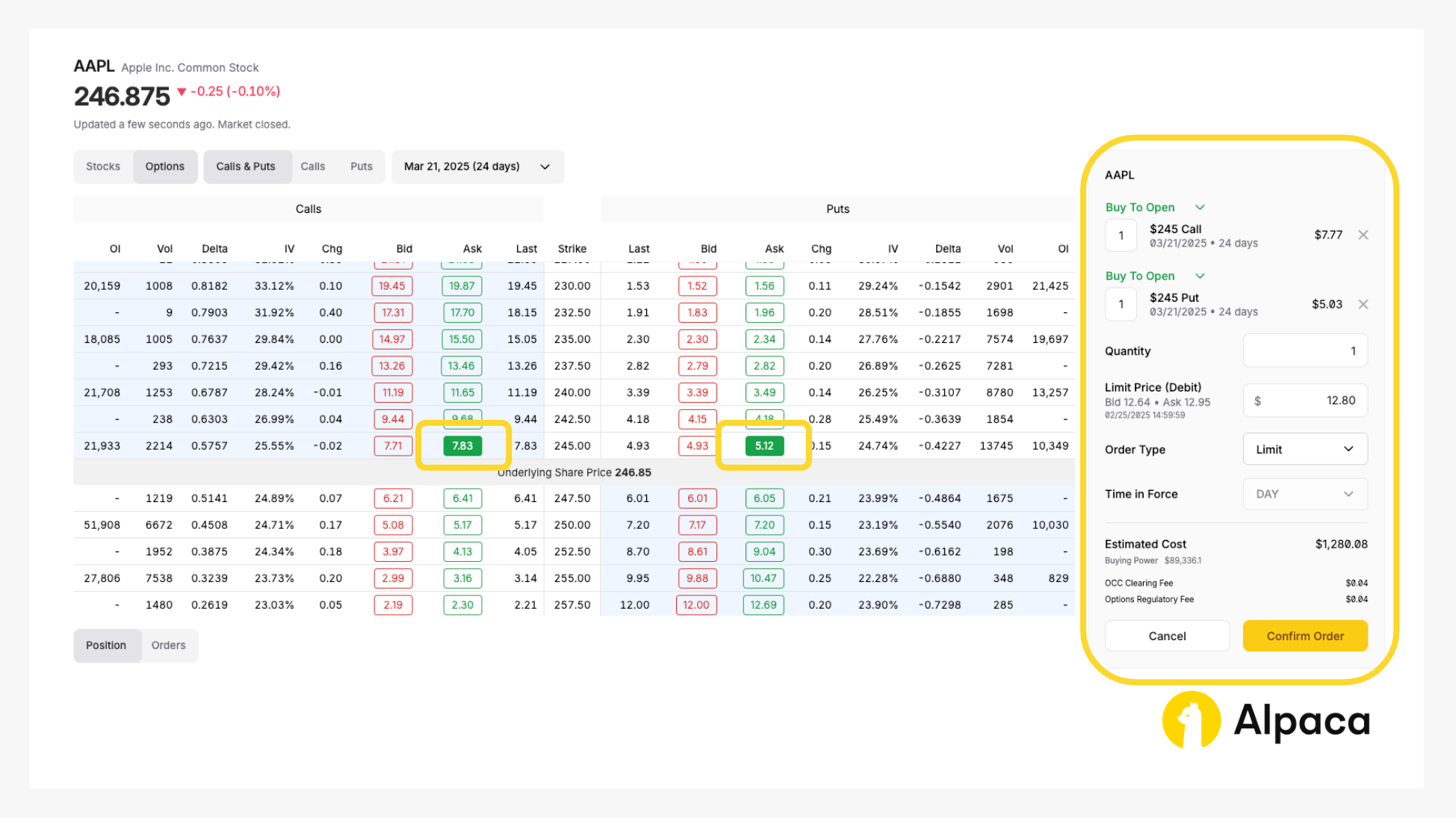
4. Opening an options position

Assume we have already analyzed the market and determined the strike price for the two legs as follows: long put option to be $245.00 and long call to be $245.00 at the expiration date of March 21, 2025. Once determined, select and review your order type (market or limit) and decide on the number of contracts you’d like to trade. You can select up to four legs but in the long straddle you only need two. 

On the asset’s page, toggle from “Stocks” to “Options” and determine your desired contract type between calls and puts. You can also adjust the expiration date from the dropdown, ranging anywhere from 0DTE options to contracts hundreds of days in the future.

A long straddle, for example, requires longing ATM (or near ATM) put and call options. Therefore, you can establish your position in the dashboard by selecting one long put option with "Buy To Open” and one long call option with “Buy To Open” to purchase the options contracts.

Please note: The order in which you select the options does not matter. Additionally, on Alpaca’s dashboard and Trading API, credits are displayed as negative values, while debits appear as positive values. For example, in the image below, a debit spread (where your initial entry requires payment) is shown with a positive limit price ($12.80 in this case) under 'Limit Price (Credit),' reflecting a total debit of -$1280.08 (with the additional costs coming from the OCC Clearing Fee and Options Regulatory Fee).

Once selected, review your order type (such as market, limit, stop, stop limit, or trailing stop) and the number of contracts you’d like to trade. Click the “Confirm Order” button on the bottom right.

Your paper trading account will then mimic the execution of the order as though it were a real transaction.

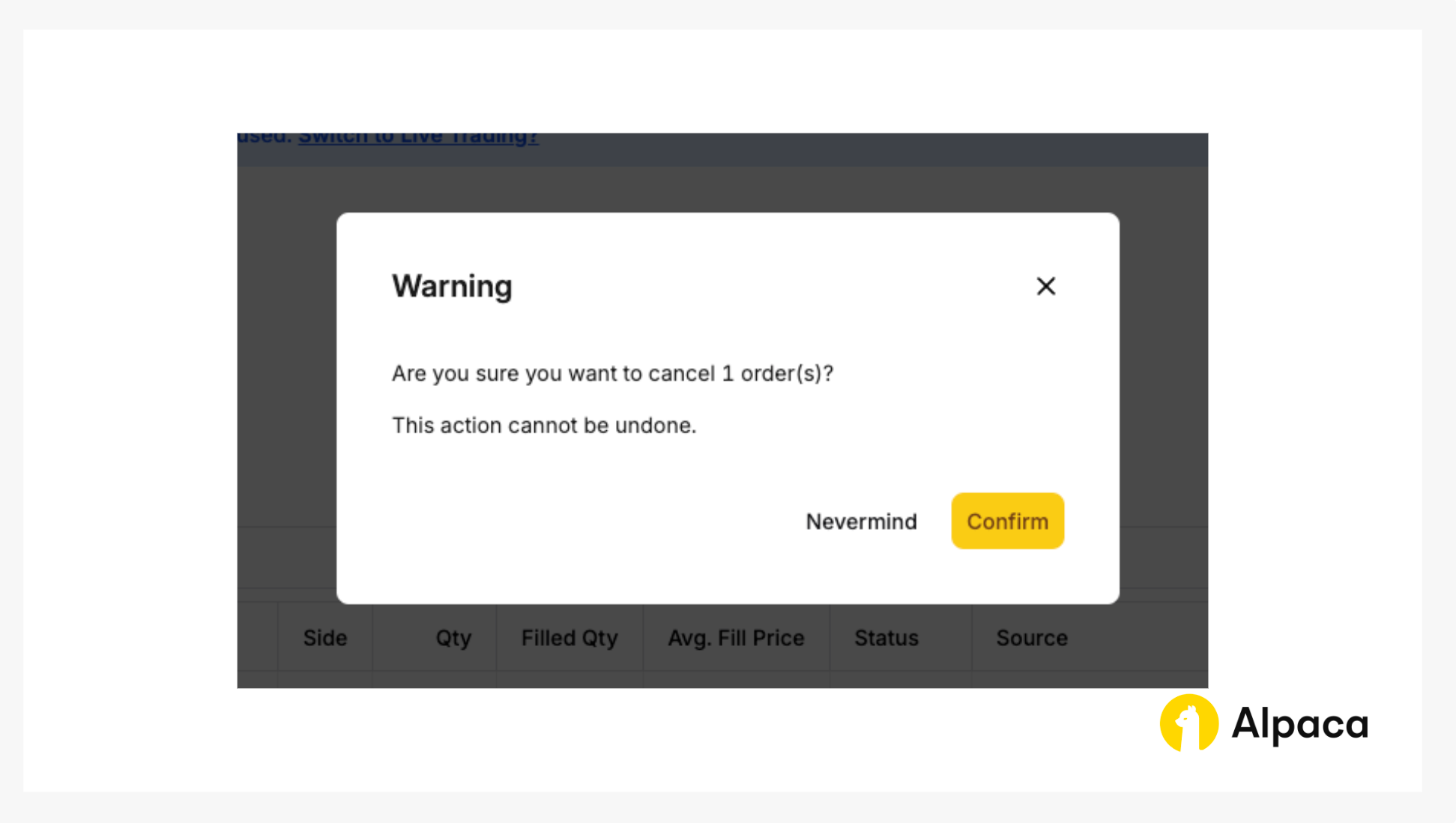
Optional: Cancel your order

Keep in mind that with a multi-leg options order, you cannot cancel or replace an individual child leg. You can only cancel or replace the entire multi-leg options order. To do this, navigate to the 'Order' section, select the order you want to cancel, and click the 'Cancel 1 selected' button.

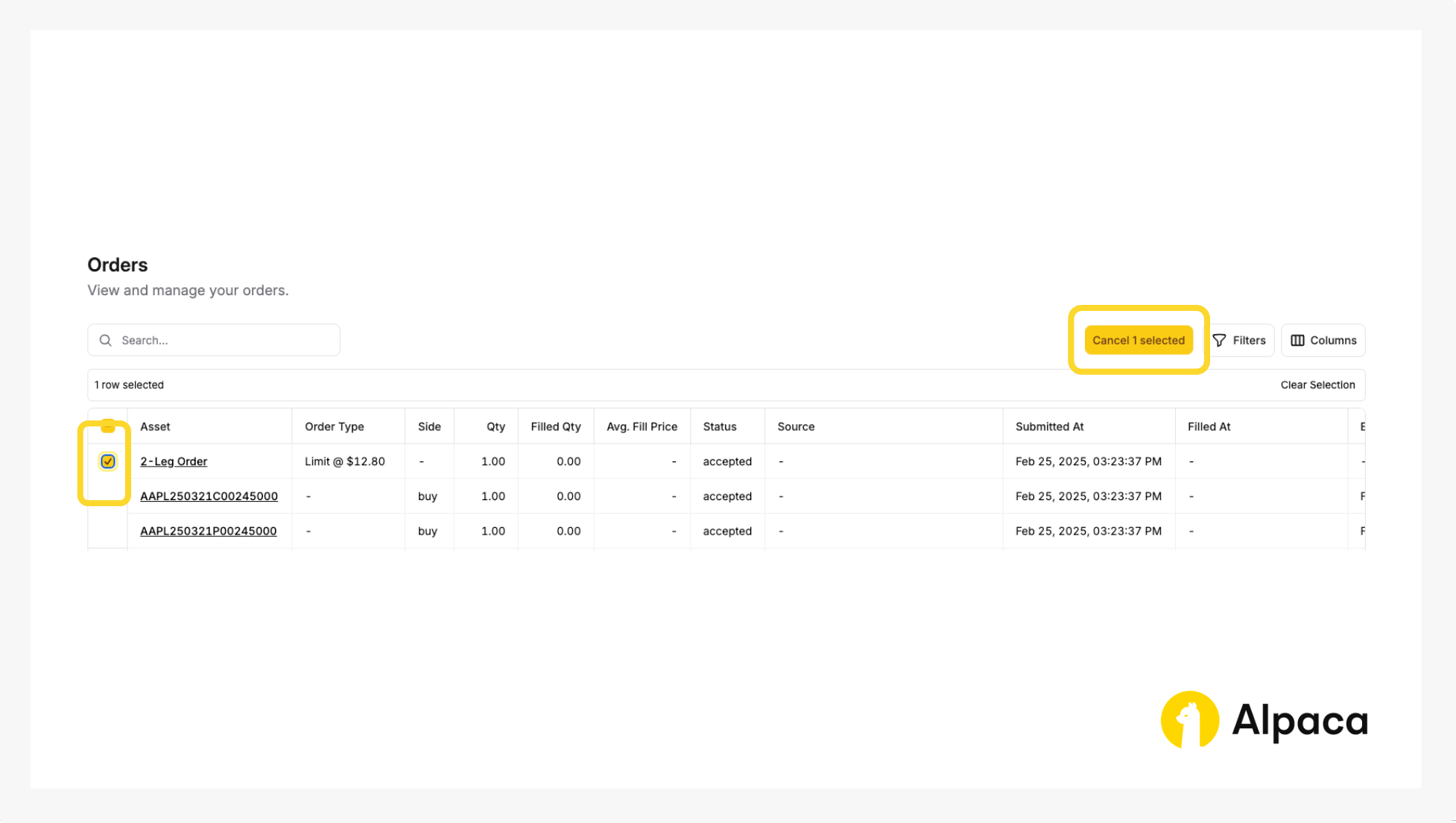
You’ll then be prompted to confirm.

5. Closing your position

Closing an options position involves selling the options contract that you previously bought (in a long position) or buying back the options contract that you previously sold (in a short position). Either action terminates, or “closes”, your associated position.

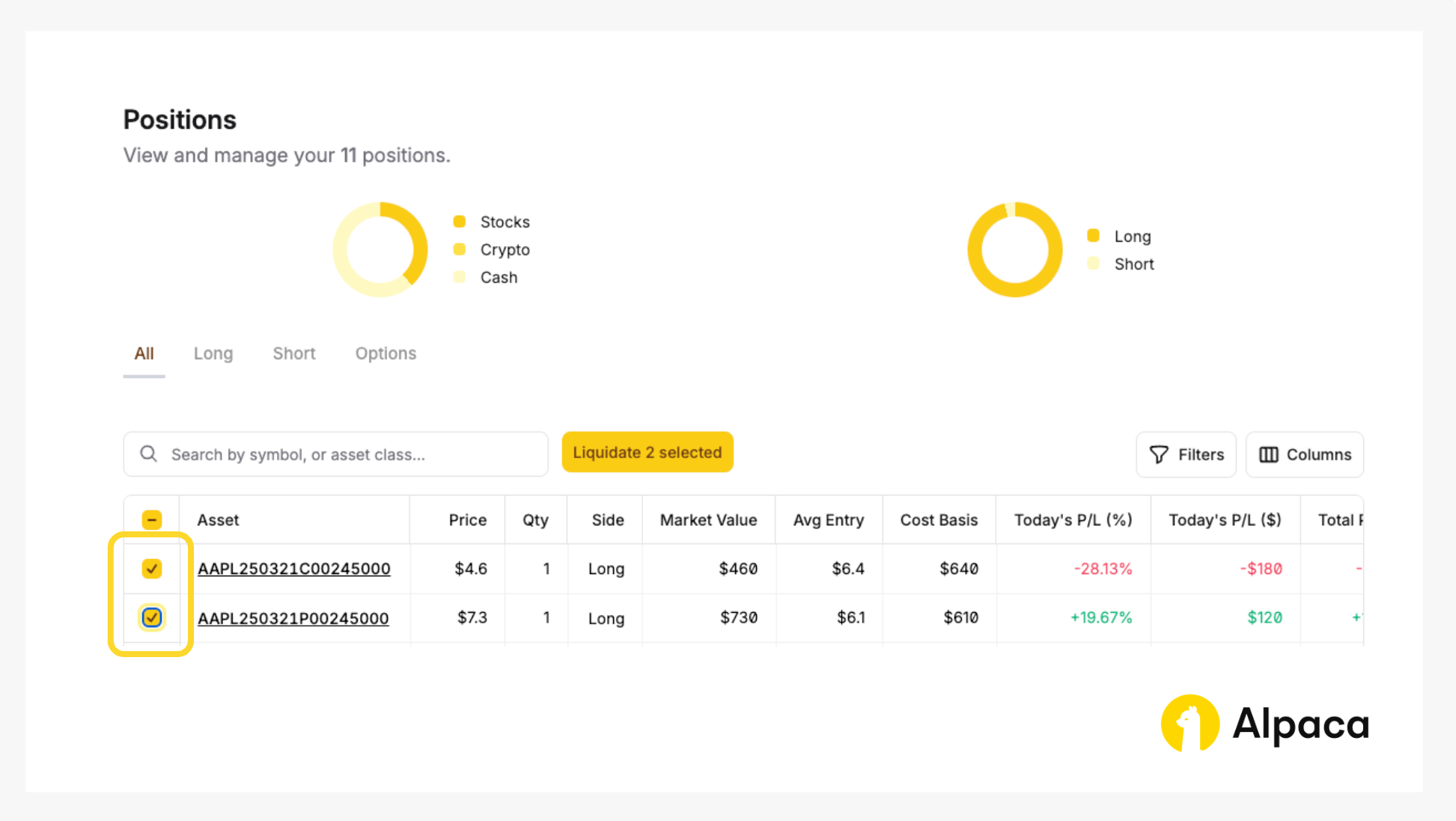
If you’d like to close your position, find the desired options contract on your “Home” page or under “Positions”. Click on the appropriate contract symbol and select “Liquidate 2 selected” to close your long straddle position.

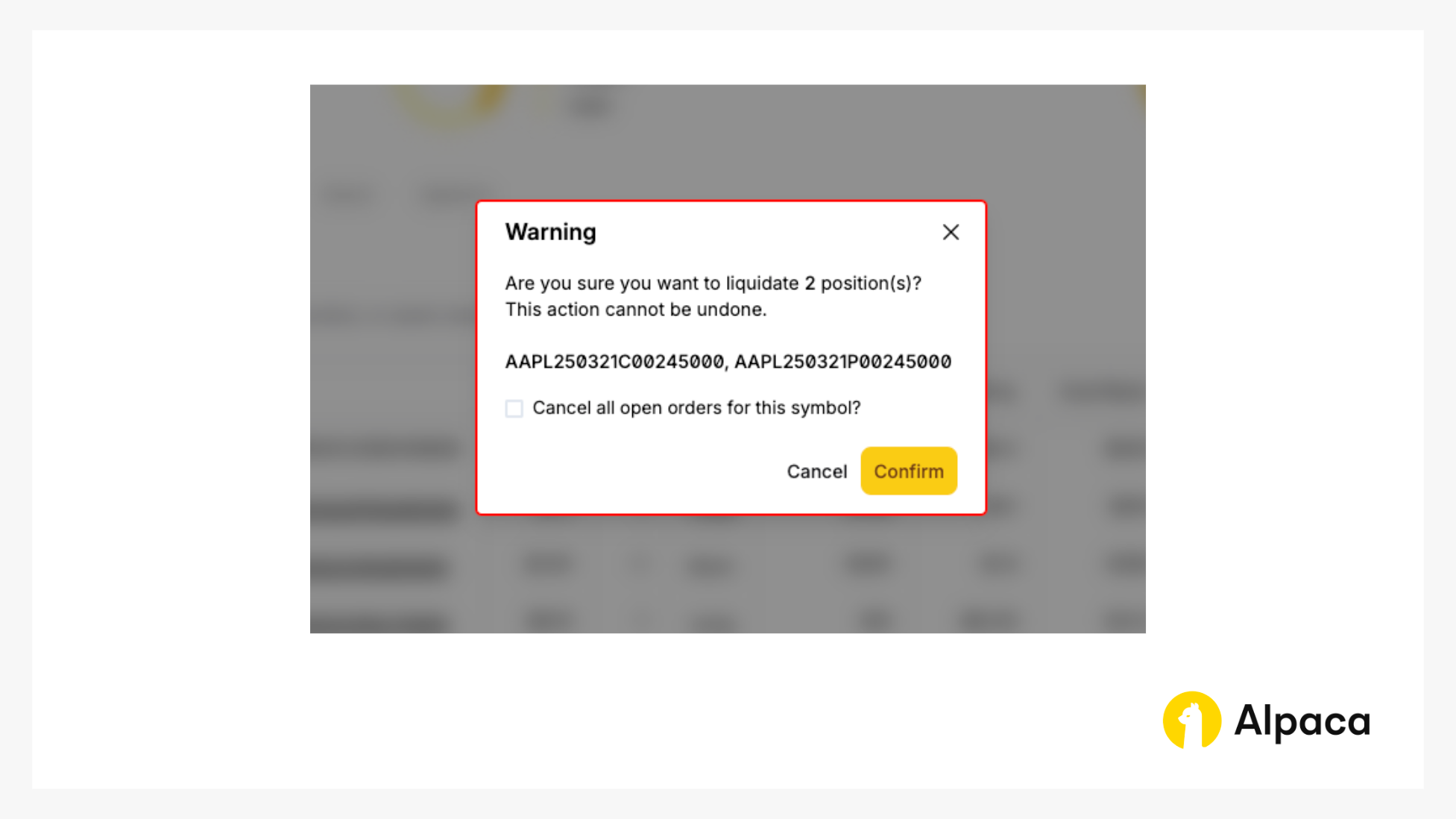
You will, then, click the “Confirm” button to liquidate the position.

Conclusion

The long straddle options strategy is one approach that traders may consider when anticipating significant price movements, regardless of direction. By purchasing both a call and a put at the same strike price, this strategy has the potential to benefit from increased volatility. It is often used in market conditions where traders expect substantial price fluctuations but are uncertain about the direction of the move.

However, executing a long straddle effectively requires an understanding of factors such as implied volatility, time decay, and market conditions. The strategy involves costs, including the total premium paid, which represents the theoretical maximum possible loss. If the underlying asset does not experience a significant price movement, time decay may erode the value of both options.

As with any advanced options strategy, a long straddle carries risks and uncertainties, and there is no guarantee of profitability. Traders should carefully evaluate the costs, monitor their positions, and consider risk management techniques such as position sizing and exit strategies. Thorough research, continuous learning, and market analysis are essential to making informed trading decisions.

For those interested in testing a long straddle strategy, tools like Alpaca’s paper trading platform can allow traders to practice in a simulated environment without financial risk.

We hope you've found this tutorial on how to trade long straddles insightful and useful for getting started on your own strategy. As you put these concepts into practice, feel free to share your feedback and experiences on our forum, Slack community, or subreddit! And don’t forget to check out the rest of our options-related tutorials.

For those looking to integrate options trading with Alpaca’s Trading API, here are some additional resources:

• Sign up for an Alpaca Trading API account
• How to Connect to Alpaca's Trading API
• How to Start Paper Trading with Alpaca's Trading API
• How to Trade Options with Alpaca’s Trading API
• Read more Options Trading Tutorials
• Documentation: Options Trading

FAQs

Is the long straddle bearish or bullish?

A long straddle is a neutral options strategy. It involves purchasing both a call and a put option with the same strike price and expiration date. This setup allows traders to potentially profit from significant price movements in either direction, making it suitable when anticipating volatility without a clear directional bias.

What are the disadvantages of a straddle?

While a long straddle offers the potential to profit from large price movements, it comes with several disadvantages:

• High Cost: Purchasing both a call and a put option can be expensive, especially when volatility is high, leading to higher premiums.
• Time Decay (Theta): As time progresses, the value of both options may erode, particularly if the underlying asset's price remains stagnant. This time decay can result in losses even if the anticipated volatility occurs later than expected.
• Requirement for Significant Price Movement: For the strategy to be profitable, the underlying asset's price must move substantially in either direction to offset the combined premiums paid. Minor fluctuations may not be sufficient to achieve breakeven.

Can you use LEAPS in long straddles?

Yes, traders can use Long-Term Equity Anticipation Securities (LEAPS) in long straddle strategies. LEAPS are options with expiration dates extending up to three years, providing a longer timeframe for the anticipated significant price movement to occur. Utilizing LEAPS in a long straddle can be advantageous when a trader expects substantial volatility over an extended period. However, it's important to note that LEAPS generally have higher premiums due to their extended duration, which increases the initial cost of implementing the strategy.

Options trading is not suitable for all investors due to its inherent high risk, which can potentially result in significant losses. Please read Characteristics and Risks of Standardized Options before investing in options.

Past hypothetical backtest results do not guarantee future returns, and actual results may vary from the analysis.

The Paper Trading API is offered by AlpacaDB, Inc. and does not require real money or permit a user to transact in real securities in the market. Providing use of the Paper Trading API is not an offer or solicitation to buy or sell securities, securities derivative or futures products of any kind, or any type of trading or investment advice, recommendation or strategy, given or in any manner endorsed by AlpacaDB, Inc. or any AlpacaDB, Inc. affiliate and the information made available through the Paper Trading API is not an offer or solicitation of any kind in any jurisdiction where AlpacaDB, Inc. or any AlpacaDB, Inc. affiliate (collectively, “Alpaca”) is not authorized to do business.

Please note that this article is for general informational purposes only and is believed to be accurate as of the posting date but may be subject to change. The examples above are for illustrative purposes only.

All investments involve risk, and the past performance of a security, or financial product does not guarantee future results or returns. There is no guarantee that any investment strategy will achieve its objectives. Please note that diversification does not ensure a profit, or protect against loss. There is always the potential of losing money when you invest in securities, or other financial products. Investors should consider their investment objectives and risks carefully before investing.

Securities brokerage services are provided by Alpaca Securities LLC ("Alpaca Securities"), member FINRA/SIPC, a wholly-owned subsidiary of AlpacaDB, Inc. Technology and services are offered by AlpacaDB, Inc.

This is not an offer, solicitation of an offer, or advice to buy or sell securities or open a brokerage account in any jurisdiction where Alpaca Securities are not registered or licensed, as applicable.