Incorporating options into your algorithmic trading can open up new strategies for profit and risk management. And while having a grasp of options trading fundamentals like calls and puts is a great foundation, understanding option Greeks may provide another layer of both complexity and opportunity.
In this article, we will discuss the five option Greeks, including what they are, how they work, and the ways they can be factored into algorithmic trading strategies.
To get the most out of this guide, explore the following resources as well:
The Five Option Greeks Explained
The option Greeks—delta, gamma, vega, theta, and rho—are mathematical measures that describe how different factors affect the price of an option. They inform you of the sensitivities of their option positions to changes in underlying variables, such as the asset price, volatility, time decay, and interest rates.
To recap, option premiums are calculated by combining the intrinsic value (based on the option's moneyness) and the extrinsic value (time until expiration, volatility, and other factors).
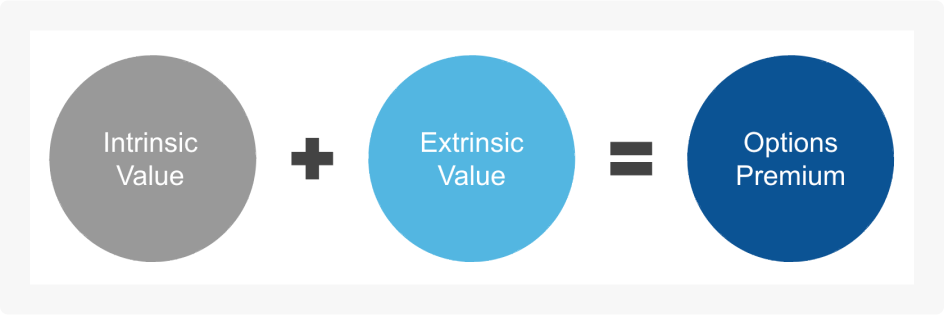
The five Greeks help quantify how different market variables influence these values, providing insights into what affects the option's price. Let’s dive into each Greek and how it works.
Delta
Delta represents the rate of change of an option's price for every $1 change in the price of the underlying asset. A delta of 0.4, for example, means that if the underlying asset's price were to increase by $1, the option's price is expected to increase by $0.40. Therefore, the higher the delta, the more the price of the option would be expected to move.

Overall, delta is measured on a scale between -1 and 1. Call options have a delta between 0 and 1, while put options range from -1 to 0.
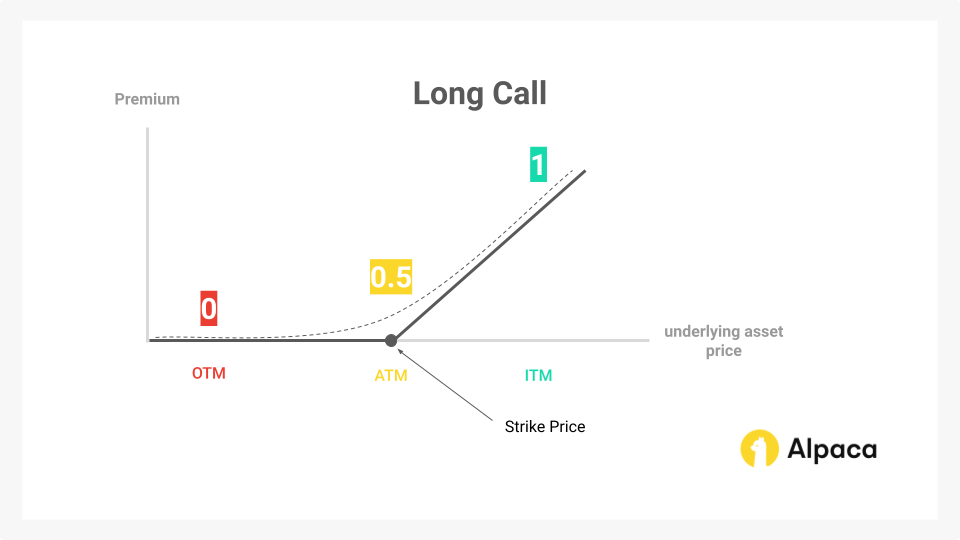
Below is an example of delta on a long call. Typically, long options benefit from greater deltas while short options often benefit from shrinking deltas. Delta also indicates the probability of an option expiring in-the-money. You can see that the delta value in a long call will move closer to 1 as its underlying asset moves ITM (in the money).
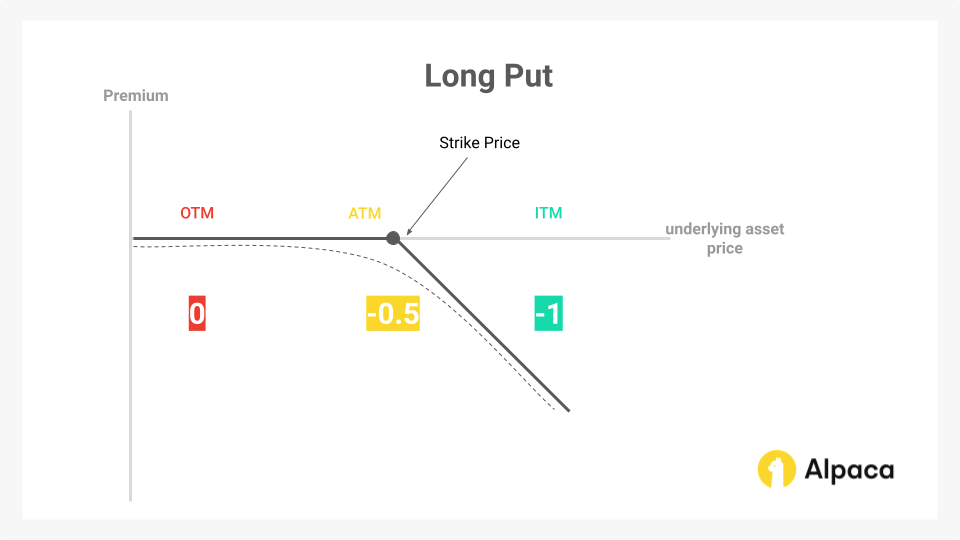
Whereas in a long put, you can see that the delta value will move closer to -1 as its underlying asset moves ITM, which is the opposite of a long call.
Because of these correlations between delta and an option’s moneyness, it is an important tool in trading strategies. For example, delta hedging is a technique used by traders to attempt to reduce or control the directional risk associated with price movements in the underlying asset by making a portfolio delta neutral. This means adjusting the portfolio's overall delta (its sensitivity to price changes) to be close to zero, so that theoretically, small price changes have less impact.
Traders could also potentially use delta to see if their portfolio is bullish or bearish. A positive total delta indicates a bullish stance, meaning the portfolio benefits if the underlying asset’s price goes up. A negative total delta suggests a bearish stance, meaning it gains if the price goes down.
Traders looking for gains from price movements typically choose high delta options for more exposure. Meanwhile, hedgers and those aiming to minimize risk might prefer low delta options to reduce sensitivity to price changes.
Let’s see how delta changes on call options in different types of moneyness (ITM, ATM, OTM). The scenario below is based on a stock (Stock A) that has a current underlying price of $260. You can see that the delta increases as the underlying stock is deeper in the money, while it decreases as the underlying stock goes out of the money.
Gamma
Gamma and delta have a very correlated relationship. This is because gamma measures the rate of change of delta in correlation to a $1 change in the underlying asset's price. Essentially, gamma indicates how delta will evolve as the market moves.

In the example of delta above, we considered an option with a delta of 0.40. If the underlying stock rises by $1, causing the option to increase by $0.40, the delta of the option is no longer 0.40. Why? This $1 move pushes the call option further in-the-money, meaning its delta should move closer to 1.00. Let’s assume the delta is now 0.55. The difference in delta, from 0.40 to 0.55, is 0.15 - this change represents the option's gamma.
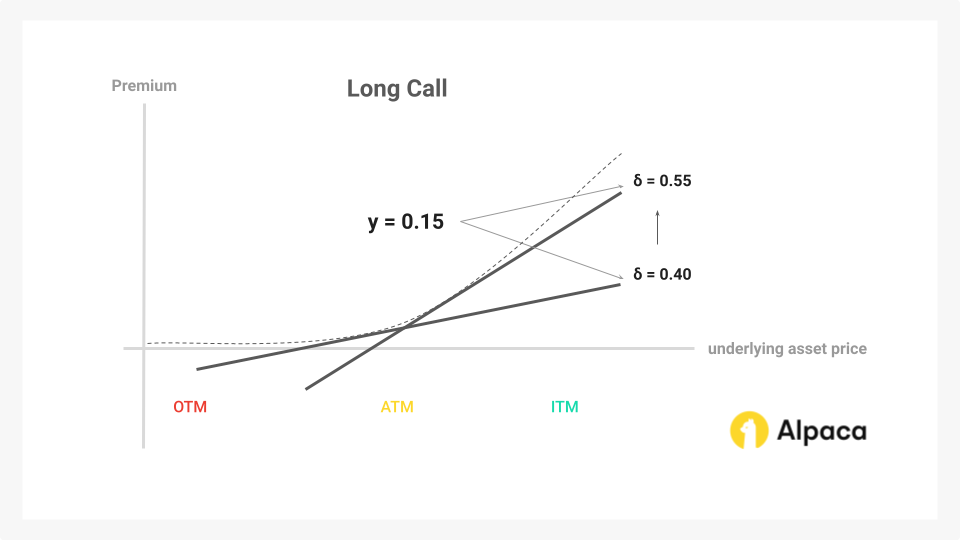
Monitoring gamma is useful for algorithmic traders because delta is not static—it changes as the underlying asset's price changes. A high gamma means that the underlying asset’s delta is highly sensitive, so a delta-neutral position can quickly become delta-positive or negative with small price moves, leading to unintended directional risk.
Failing to account for gamma can cause significant discrepancies between expected and actual performance. Therefore, algorithms must monitor gamma to anticipate how delta will evolve with price movements. High gamma options often cause deltas to change rapidly, requiring frequent rebalancing to maintain delta neutrality—this is known as dynamic hedging.
Short-term traders and scalpers could benefit from the leverage effect of high gamma, capitalizing on quick price movements. On the other hand, long-term investors may prefer lower gamma to reduce the need for frequent rebalancing.
Going back to the same Stock A example in the delta section above, you can see that typically, gamma is highest when an option is ATM (at the money). When an option is OTM or deep ITM, the premium is generally lower, and gamma is also smaller (e.g., 0.008), indicating a slower rate of change in delta. This lower gamma means that OTM options have less sensitivity to price movements, contributing to their lower premium.
Vega
Vega measures how much an option's price changes when implied volatility (IV) shifts by one percent (1%). Implied volatility, much like how it sounds, represents the market’s expectations for future price movements. When the IV of the underlying asset rises, the option’s premium increases because there’s a higher chance it will end up profitable or ITM. When the IV of the security decreases, so will the premium.

Unlike delta, which behaves differently for calls and puts, vega is always positive. This means that when IV goes up, it typically raises the portion of the premium driven by volatility, whether it’s a call or a put, and decreases when IV goes down. For example, if Stock A’s IV rises by one percent and a call option has a vega of 0.70, the premium will increase by $0.70.
Higher IV typically indicates greater market uncertainty and larger potential price swings, while a lower IV may suggest stability and smaller movements. Traders may attempt to exploit these changes in volatility using various strategies, however, none of them are guaranteed to return positive results:
- Volatility Trading: Algorithms can be used to detect potential patterns or events, such as earnings announcements or economic reports, that might cause volatility spikes.
- Volatility Arbitrage: Traders could hypothetically profit from differences between implied and historical volatility by betting that these discrepancies will narrow.
- Dynamic Vega Hedging: Traders could adjust portfolios to keep a preferred level of exposure to volatility, increasing it when they expect profits and decreasing it when risks rise.
For example, traders who expect increased volatility may choose options with high vega because they typically gain more as premiums rise. On the other hand, those anticipating stable or lower volatility may prefer options with low vega to limit the risk of losing value from falling IV. At the end of the day, it is up to the trader what strategies they want to use.
Options with longer expiration dates often have higher vega, as there’s more time for volatility to affect their value. As expiration approaches, vega tends to gradually decrease.
Let’s take an example using Stock A’s call options. Suppose we have three call options with the following details:
Even with the same strike price, the premium can vary depending on the days to expiration (DTE). Options with more days left tend to have higher premiums partly because their IV is higher and so vega is.
Theta
Theta represents how much value an option loses each day due to the passage of time, specifically measuring the time decay component of an option's premium (its extrinsic value). An option with a theta of -0.04, for example, loses $0.04 in premium daily.

Who possibly benefits from a high theta in trading? Theta is usually negative for option holders. This is because as expiration nears, options lose value faster, impacting buyers negatively but benefiting sellers. The effects of time decay are not always linear.
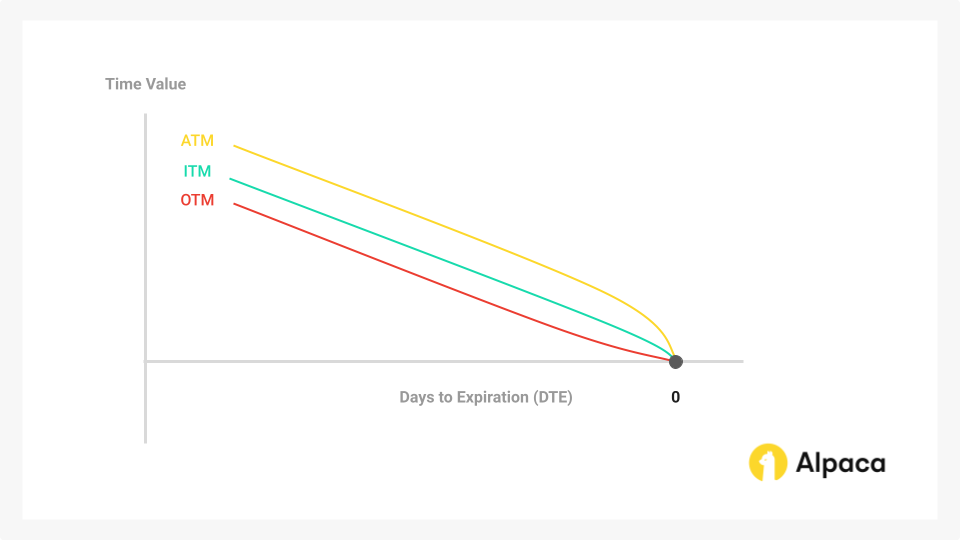
We can observe this effect in the same call options chain of stock A.
Given these characteristics, algorithms can try implementing various theta-based strategies. Option sellers typically benefit from high theta, profiting from time decay by selling options in order to profit off of premiums. Conversely, option buyers usually prefer low thetas to minimize value erosion. Algorithms could be built to factor theta into expected returns and adjust positions to offset potential theta losses.
Rho
Rho measures how much an option's price changes with a one percent shift in interest rates. It reflects the sensitivity of the option's premium to these rate changes. For call options, rho is positive - when interest rates rise, call premiums typically increase. Conversely, put options have negative rho, meaning their premiums tend to decrease as rates rise.
Interest rates affect option premiums through opportunity cost and the present value of the exercise price. When interest rates are high, the present value of the exercise price decreases, making calls more valuable and puts less valuable. This is because a call option doesn’t require paying the full price of the stock right away, allowing the investor to potentially earn interest on the cash that isn’t tied up in the stock.

Rho is often considered more relevant for longer-term options. As rates rise, the cost of holding options increases. Typically, traders with call options benefit from high rho as premiums rise with rates, while put option holders typically prefer low rho to limit premium loss when rates fall.
Traders often incorporate rho into strategies if they expect rate changes:
- Interest Rate Trading: Expecting rate hikes, traders could choose options with high rho to capitalize on rising premiums.
- Long-Term Strategies: Investors holding long-term options typically monitor rho, anticipating how rate shifts may affect their positions.
For instance, let's consider an options chain for Stock A. Suppose we have three call options with the following details:
Options with longer expirations have higher rho, making them more sensitive to rate changes. In this example, if rates were to rise by 1%, the longest-dated option (rho = 0.54) would see a $0.54 premium increase, while options with shorter durations show smaller adjustments. Conversely, options with shorter durations, like the one with a rho of 0.19, typically show less sensitivity to interest rate changes, leading to smaller adjustments in their premiums.
Using Option Greeks In Algorithmic Trading
Using algorithms to incorporate the Greeks in options trading offers key advantages. They allow for precise measurement of an option’s risk sensitivity, reducing human error and minimizing emotional influence on trading decisions.
Real-Time Monitoring and Reaction
Option Greeks fluctuate continuously due to dynamic market conditions. Algorithms can process real-time data and respond to even subtle changes in Greeks like delta, vega, or gamma with exceptional speed and accuracy. This automation enables algorithms to adjust positions almost instantaneously, aligning them with current market conditions. Such capability is critical for strategies that require rapid recalibration, like maintaining delta-neutrality.
However, this reliance on real-time data and rapid execution can also introduce risks. For instance, algorithms may be susceptible to market noise and short-term fluctuations, leading to excessive trading and increased transaction costs. Additionally, in the event of market disruptions or technical glitches, the algorithm's ability to react in a timely and accurate manner could be compromised, potentially resulting in unintended consequences. It is essential to carefully design and test algorithms to ensure they can effectively navigate these challenges while capitalizing on the benefits of real-time monitoring and reaction.
Managing Gamma Exposure
Traders may employ strategies such as gamma scalping, systematically adjusting their delta to capitalize on gamma fluctuations in response to price movements of the underlying asset. Algorithms can automate this process, ensuring that the trader efficiently captures incremental gains without the necessity of continuous position monitoring and adjustment.
Conversely, negative gamma exposure can potentially lead to substantial and rapid losses in the event of abrupt price movements in the underlying asset. An algorithm can continuously monitor gamma risk and, if necessary, automatically reduce positions to mitigate potential losses.
Efficient Time Decay (Theta) Management
As theta demonstrates, options lose value as the expiration date approaches. Algorithms can be designed to track theta exposure, enabling traders to manage the effects of time decay more effectively. These algorithms can be programmed to establish exit positions at favorable times, preventing excessive holding periods. This proactive approach to managing time decay risk allows for the closure of positions before they become a liability due to accelerated theta decay.
Dynamic Vega and Volatility Exposure Adjustments
In volatile markets, option values can fluctuate significantly, impacting vega exposure. An algorithm can instantaneously adjust positions in response to changes in implied volatility, enabling traders to capitalize on volatility spikes or mitigate losses when volatility decreases. For volatility-sensitive positions, such as long straddles, maintaining appropriate vega exposure is crucial. Algorithms can continuously adjust these positions, hedging or increasing vega exposure as necessary to align with prevailing market volatility.
However, the effectiveness of vega hedging strategies can be influenced by the accuracy of the implied volatility model used, as discrepancies between model predictions and actual volatility can lead to unintended risk exposures.
Position Adjustments Based on Interest Rate Sensitivity
Although rho is often a minor consideration, it is more significant at times where interest rates are expected to fluctuate. Algorithms can be built to factor rho into their calculations and make small adjustments as needed to account for interest rate changes, ensuring the trader’s position aligns with their risk tolerance and goals.
However, it's important to remember that interest rate movements can be unpredictable. Unexpected shifts in rates can lead to inaccurate rho calculations and unintended consequences for option positions. Additionally, the impact of rho can vary significantly depending on the specific option and market conditions. In some cases, the effect of interest rate changes on option prices may be minimal, limiting the effectiveness of rho-based adjustments.
Managing Multi-Greek Considerations
As emphasized throughout this article, the Greeks exhibit interdependencies; optimizing for one Greek necessitates consideration of its impact on others. For instance, an increase in gamma often corresponds to accelerated theta decay. Algorithms can facilitate the balancing of multiple Greeks within a portfolio, ensuring that no single risk factor becomes disproportionately large without the trader's explicit intent.
Algorithms can be designed to trigger alerts or execute trades if a Greek surpasses a predetermined threshold– safeguarding against unforeseen and undesirable risk exposures, such as excessive gamma or vega.
Backtesting and Optimization of Greek Sensitivity
Individual traders may have varying preferences regarding the incorporation of Greeks into their algorithmic trading strategies. Algorithms can be employed to backtest the performance of Greek-based strategies under diverse market conditions. This analysis facilitates visualization and refinement of strategies, enabling traders to gain a deeper understanding of how their positions would have responded to fluctuations in the Greeks.
When Manual Trading the Greeks Could Make Sense
While algorithmic trading offers superior efficiency in managing Greek exposure over the long term, manual trading retains its value in certain scenarios. For example, while algorithmic trading excels in rapid responses to market fluctuations, manual trading provides a safeguard against unintended automated actions. This highlights the critical importance of thorough backtesting and gradual implementation of changes within algorithmic trading frameworks.
Additionally, the complex relationship among the Greeks can require a steep learning curve to fully understand the profit potential tied to each individual one. Trading manually, at least initially, can facilitate a deeper understanding of each Greek’s nuanced effects on option moneyness. This foundational understanding can then inform the development and backtesting of algorithmic strategies– ultimately enhancing trading speed while capitalizing on opportunities more effectively.
Conclusion
In summary, while both algorithmic and manual trading can benefit from understanding and applying the Greeks, each approach has its strengths. Algorithmic trading can offer advantages in speed, precision, and real-time response, which may be beneficial in fast or volatile markets. Manual trading, however, may be better suited to simpler, lower-frequency strategies that do not require constant adjustments.
By understanding the unique capabilities and limitations of each approach, traders can align their strategies with their preferred methods of trading.
Curious to learn more about algorithmic trading? Check out more of our resources on algorithmic trading.
Options trading is not suitable for all investors due to its inherent high risk, which can potentially result in significant losses. Please read Characteristics and Risks of Standardized Options before investing in options.
Past hypothetical backtest results do not guarantee future returns, and actual results may vary from the analysis.
Please note that this article is for general informational purposes only and is believed to be accurate as of the posting date but may be subject to change. The examples above are for illustrative purposes only.
All investments involve risk, and the past performance of a security, or financial product does not guarantee future results or returns. There is no guarantee that any investment strategy will achieve its objectives. Please note that diversification does not ensure a profit, or protect against loss. There is always the potential of losing money when you invest in securities, or other financial products. Investors should consider their investment objectives and risks carefully before investing.
Securities brokerage services are provided by Alpaca Securities LLC ("Alpaca Securities"), member FINRA/SIPC, a wholly-owned subsidiary of AlpacaDB, Inc. Technology and services are offered by AlpacaDB, Inc.
This is not an offer, solicitation of an offer, or advice to buy or sell securities or open a brokerage account in any jurisdiction where Alpaca Securities are not registered or licensed, as applicable.